Note
Go to the end to download the full example code
1D Forward Simulation with Chargeable and/or Magnetic Viscosity#
Here we use the module SimPEG.electromangetics.time_domain_1d to compare predicted time domain data for a single sounding when the Earth is purely conductive, chargeable and/or magnetically viscous. In this tutorial, we focus on:
Defining receivers, sources, waveform and the survey
Defining physical properties when the Earth is chargeable and/or magnetically viscous
Setting physical property values as constant in the simulation
Our survey geometry consists of a horizontal loop source with a radius of 10 m located 0.5 m above the Earth’s surface. The receiver is located at the centre of the loop and measures the vertical component of the response.
Import Modules#
import numpy as np
from matplotlib import pyplot as plt
from SimPEG import maps
import SimPEG.electromagnetics.time_domain as tdem
from SimPEG.electromagnetics.utils.em1d_utils import ColeCole, LogUniform
# sphinx_gallery_thumbnail_number = 3
Create Survey#
Here we demonstrate a general way to define the receivers, sources, waveforms and survey. For this tutorial, the source is a horizontal loop whose current waveform is a unit step-off. Receivers are defined to measure the vertical component of the magnetic flux density and its time-derivative at the loop’s center.
source_location = np.array([0.0, 0.0, 0.5])
source_orientation = "z" # "x", "y" or "z"
current_amplitude = 1.0 # maximum amplitude of source current
source_radius = 10.0 # loop radius
receiver_location = np.array([0.0, 0.0, 0.5])
receiver_orientation = "z" # "x", "y" or "z"
times = np.logspace(-6, -1, 51) # time channels (s)
# Receiver list
receiver_list = []
receiver_list.append(
tdem.receivers.PointMagneticFluxDensity(
receiver_location, times, orientation=receiver_orientation
)
)
receiver_list.append(
tdem.receivers.PointMagneticFluxTimeDerivative(
receiver_location, times, orientation=receiver_orientation
)
)
# Waveform
waveform = tdem.sources.StepOffWaveform()
# Sources
source_list = [
tdem.sources.CircularLoop(
receiver_list=receiver_list,
location=source_location,
waveform=waveform,
current=current_amplitude,
radius=source_radius,
)
]
# Survey
survey = tdem.Survey(source_list)
Defining a 1D Layered Earth Model#
Here, we define the layer thicknesses and physical properties for our 1D simulation. If we have N layers, parameters for the physical properties must be defined for each layer and we must provide N-1 layer thicknesses. The lowest layer is assumed to extend to infinity.
For this tutorial, we predict the response for a halfspace model, however the script has been generalized to work for an arbitrary number of layers. If the Earth is a halfspace, the thicknesses could instead be defined by an empty array, and each physical property value by an array of length 1.
# Layer thicknesses
thicknesses = np.array([40.0, 40.0])
n_layer = len(thicknesses) + 1
# In SimPEG, the Cole-Cole model is used to define a frequency-dependent
# electrical conductivity when the Earth is chargeable.
sigma = 1e-1 # infinite conductivity in S/m
eta = 0.5 # intrinsice chargeability [0, 1]
tau = 0.01 # central time-relaxation constant in seconds
c = 0.75 # phase constant [0, 1]
# In SimPEG, the a log-uniform distribution of time-relaxation constants is used
# to define a frequency-dependent susceptibility when the Earth exhibits
# magnetic viscosity
chi = 0.001 # infinite susceptibility in SI
dchi = 0.001 # amplitude of frequency-dependent susceptibility contribution
tau1 = 1e-7 # lower limit for time relaxation constants in seconds
tau2 = 1.0 # upper limit for time relaxation constants in seconds
# For each physical property, the parameters must be defined for each layer.
# In this case, we must define all parameters for the Cole-Cole conductivity
# as well as the frequency-dependent magnetic susceptibility.
sigma_model = sigma * np.ones(n_layer)
eta_model = eta * np.ones(n_layer)
tau_model = tau * np.ones(n_layer)
c_model = c * np.ones(n_layer)
chi_model = chi * np.ones(n_layer)
dchi_model = dchi * np.ones(n_layer)
tau1_model = tau1 * np.ones(n_layer)
tau2_model = tau2 * np.ones(n_layer)
# Here, we let the infinite conductivity be the model. As a result, we only
# need to define the mapping for this parameter. All other parameters used
# to define physical properties will be fixed when creating the simulation.
model_mapping = maps.IdentityMap(nP=n_layer)
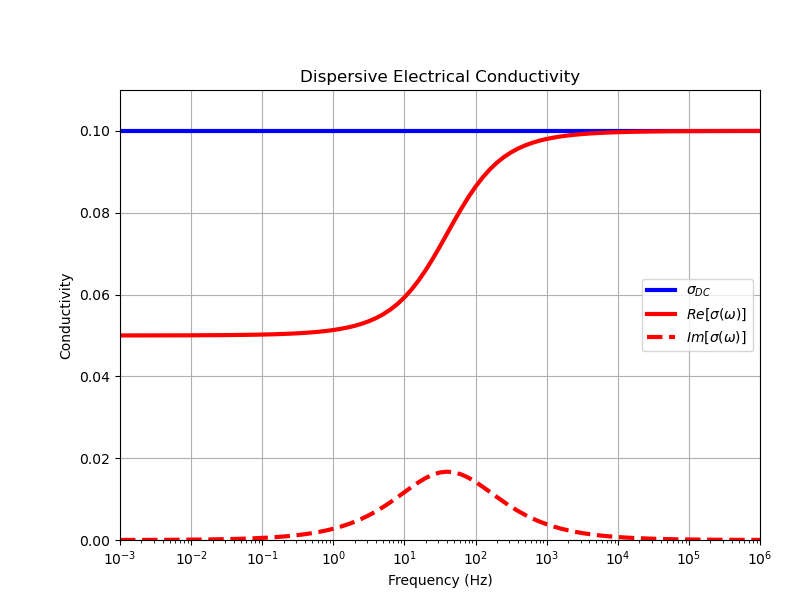
# Compute and plot complex conductivity at all frequencies
frequencies = np.logspace(-3, 6, 91)
sigma_complex = ColeCole(frequencies, sigma, eta, tau, c)
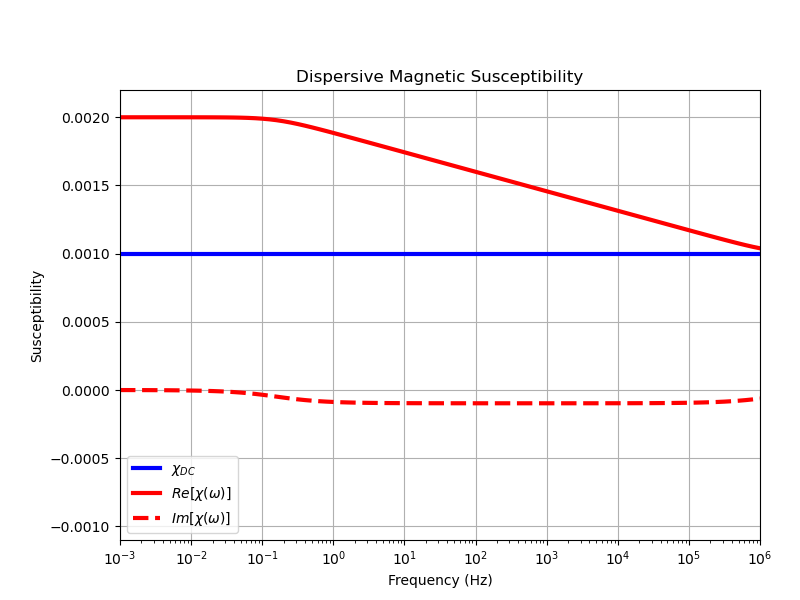
chi_complex = LogUniform(frequencies, chi, dchi, tau1, tau2)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_axes([0.15, 0.1, 0.8, 0.75])
ax.semilogx(frequencies, sigma * np.ones(len(frequencies)), "b", lw=3)
ax.semilogx(frequencies, np.real(sigma_complex), "r", lw=3)
ax.semilogx(frequencies, np.imag(sigma_complex), "r--", lw=3)
ax.grid()
ax.set_xlim(np.min(frequencies), np.max(frequencies))
ax.set_ylim(0.0, 1.1 * sigma)
ax.set_xlabel("Frequency (Hz)")
ax.set_ylabel("Conductivity")
ax.set_title("Dispersive Electrical Conductivity")
ax.legend(
[r"$\sigma_{DC}$", r"$Re[\sigma (\omega)]$", r"$Im[\sigma (\omega)]$"],
loc="center right",
)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_axes([0.15, 0.1, 0.8, 0.75])
ax.semilogx(frequencies, chi * np.ones(len(frequencies)), "b", lw=3)
ax.semilogx(frequencies, np.real(chi_complex), "r", lw=3)
ax.semilogx(frequencies, np.imag(chi_complex), "r--", lw=3)
ax.grid()
ax.set_xlim(np.min(frequencies), np.max(frequencies))
ax.set_ylim(-1.1 * chi, 1.1 * (chi + dchi))
ax.set_xlabel("Frequency (Hz)")
ax.set_ylabel("Susceptibility")
ax.set_title("Dispersive Magnetic Susceptibility")
ax.legend(
[r"$\chi_{DC}$", r"$Re[\chi (\omega)]$", r"$Im[\chi (\omega)]$"], loc="lower left"
)
<matplotlib.legend.Legend object at 0x7f36b5e4dd60>
Define the Forward Simulation and Predict Data#
Here we predict the TDEM sounding for several halfspace models (conductive, chargeable, magnetically viscous). Since the physical properties defining the Earth are different, it requires a separate simulation object be created for each case. Each simulation requires the user define the survey, the layer thicknesses and a mapping.
A universal mapping was created by letting sigma be the model. All other parameters used to define the physical properties are permanently set when defining the simulation.
When using the SimPEG.electromagnetics.time_domain_1d module, note that predicted data are organized by source, then by receiver, then by time channel.
# Simulate response for static conductivity
simulation_conductive = tdem.Simulation1DLayered(
survey=survey, thicknesses=thicknesses, sigmaMap=model_mapping
)
dpred_conductive = simulation_conductive.dpred(sigma_model)
# Simulate response for a chargeable Earth
simulation_chargeable = tdem.Simulation1DLayered(
survey=survey,
thicknesses=thicknesses,
sigmaMap=model_mapping,
eta=eta,
tau=tau,
c=c,
)
dpred_chargeable = simulation_chargeable.dpred(sigma_model)
# Simulate response for viscous remanent magnetization
mu0 = 4 * np.pi * 1e-7
mu = mu0 * (1 + chi)
simulation_vrm = tdem.Simulation1DLayered(
survey=survey,
thicknesses=thicknesses,
sigmaMap=model_mapping,
mu=mu,
dchi=dchi,
tau1=tau1,
tau2=tau2,
)
dpred_vrm = simulation_vrm.dpred(sigma_model)
/home/vsts/conda/envs/simpeg-test/lib/python3.8/site-packages/numpy/core/_asarray.py:130: ComplexWarning:
Casting complex values to real discards the imaginary part
Plotting Results#
fig = plt.figure(figsize=(12, 5))
ax1 = fig.add_axes([0.1, 0.1, 0.38, 0.85])
ax1.loglog(times, np.abs(dpred_conductive[0 : len(times)]), "k", lw=3)
ax1.loglog(times, np.abs(dpred_chargeable[0 : len(times)]), "r", lw=3)
ax1.loglog(times, np.abs(dpred_vrm[0 : len(times)]), "b", lw=3)
ax1.set_xlim([times.min(), times.max()])
ax1.grid()
ax1.legend(["Purely Inductive", "Chargeable", "Magnetically Viscous"])
ax1.set_xlabel("Times (s)")
ax1.set_ylabel("|B| (T)")
ax1.set_title("Magnetic Flux")
ax2 = fig.add_axes([0.6, 0.1, 0.38, 0.85])
ax2.loglog(times, np.abs(dpred_conductive[len(times) :]), "k", lw=3)
ax2.loglog(times, np.abs(dpred_chargeable[len(times) :]), "r", lw=3)
ax2.loglog(times, np.abs(dpred_vrm[len(times) :]), "b", lw=3)
ax2.set_xlim([times.min(), times.max()])
ax2.grid()
ax2.legend(["Purely Inductive", "Chargeable", "Magnetically Viscous"])
ax2.set_xlabel("Times (s)")
ax2.set_ylabel("|dB/dt| (T/s)")
ax2.set_title("Time-Derivative of Magnetic Flux")
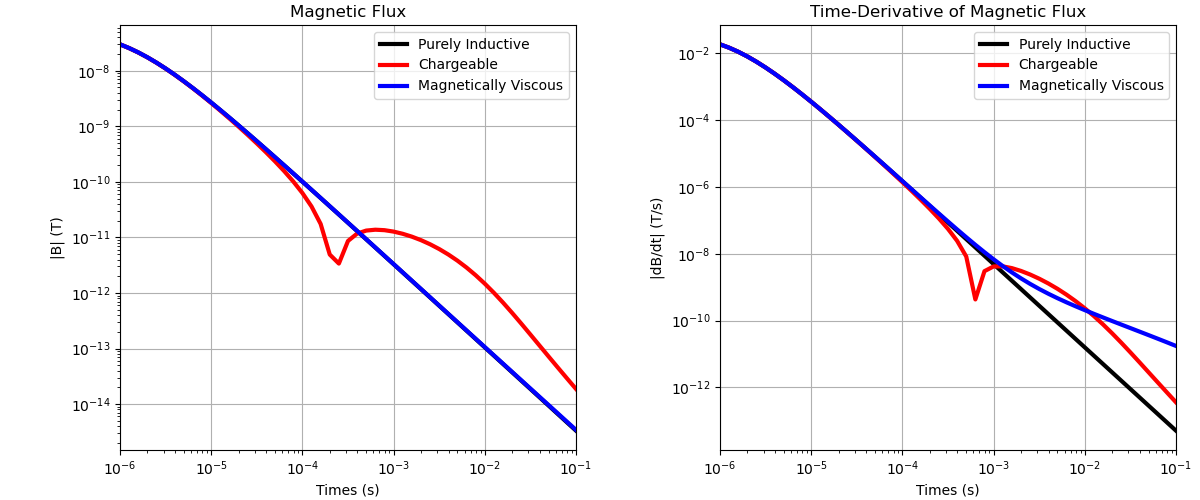
Text(0.5, 1.0, 'Time-Derivative of Magnetic Flux')
Total running time of the script: (0 minutes 4.812 seconds)
Estimated memory usage: 8 MB