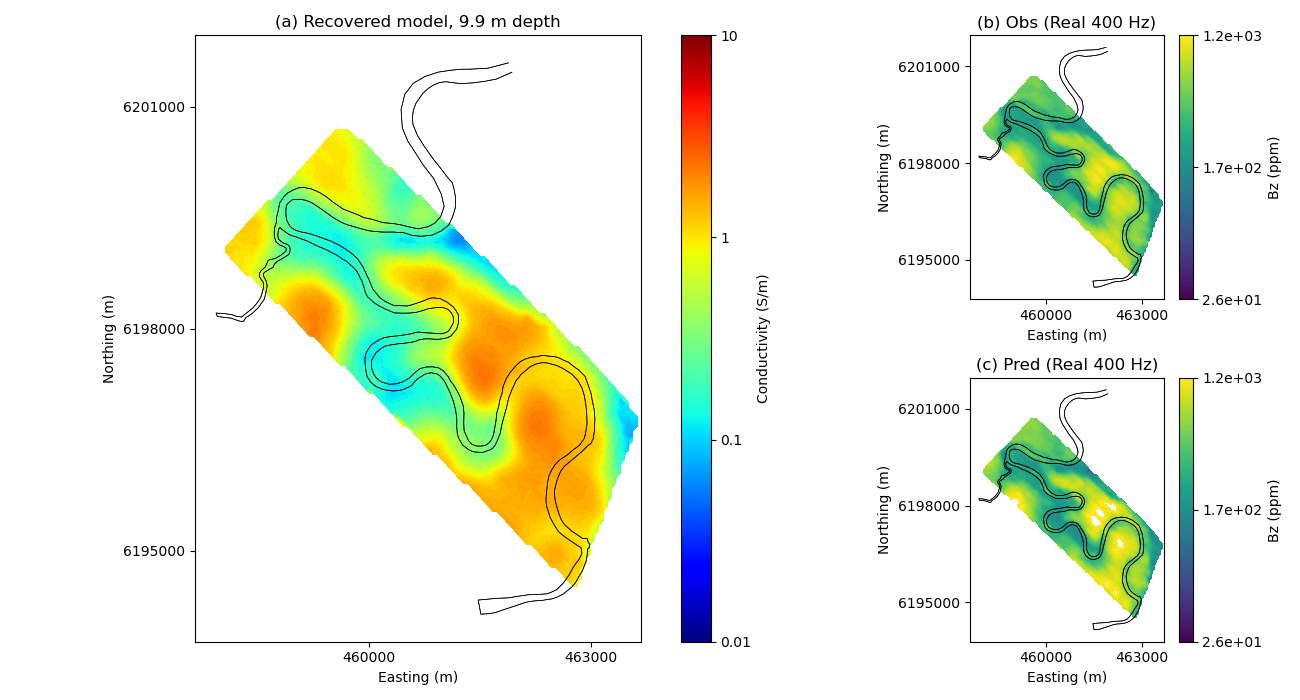
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion

In this example, perform a stitched 1D inversion of the Bookpurnong RESOLVE data. The original data can be downloaded from: https://storage.googleapis.com/simpeg/bookpurnong/bookpurnong.tar.gz

The forward simulation is performed on the cylindrically symmetric mesh using SimPEG.electromagnetics.frequency_domain.

Lindsey J. Heagy, Rowan Cockett, Seogi Kang, Gudni K. Rosenkjaer, Douglas W. Oldenburg, A framework for simulation and inversion in electromagnetics, Computers & Geosciences, Volume 107, 2017, Pages 1-19, ISSN 0098-3004, http://dx.doi.org/10.1016/j.cageo.2017.06.018.

The script and figures are also on figshare: https://doi.org/10.6084/m9.figshare.5107711

This example was updated for SimPEG 0.14.0 on January 31st, 2020 by Joseph Capriotti

Downloading https://storage.googleapis.com/simpeg/bookpurnong/bookpurnong_inversion.tar.gz
   saved to: /home/vsts/work/1/s/examples/20-published/bookpurnong_inversion.tar.gz
Download completed!
-1186.799999353935 223.59999987827757
25.714073250740157 1150.0071749097713

import h5py
import tarfile
import os
import shutil
import numpy as np
import matplotlib.pyplot as plt

from pymatsolver import PardisoSolver
from scipy.constants import mu_0
from scipy.spatial import cKDTree

import discretize
from SimPEG import (
    maps,
    utils,
    data_misfit,
    regularization,
    optimization,
    inversion,
    inverse_problem,
    directives,
    data,
)
from SimPEG.electromagnetics import frequency_domain as FDEM


def download_and_unzip_data(
    url="https://storage.googleapis.com/simpeg/bookpurnong/bookpurnong_inversion.tar.gz",
):
    """
    Download the data from the storage bucket, unzip the tar file, return
    the directory where the data are
    """
    # download the data
    downloads = utils.download(url)

    # directory where the downloaded files are
    directory = downloads.split(".")[0]

    # unzip the tarfile
    tar = tarfile.open(downloads, "r")
    tar.extractall()
    tar.close()

    return downloads, directory


def resolve_1Dinversions(
    mesh,
    dobs,
    src_height,
    freqs,
    m0,
    mref,
    mapping,
    relative=0.08,
    floor=1e-14,
    rxOffset=7.86,
):
    """
    Perform a single 1D inversion for a RESOLVE sounding for Horizontal
    Coplanar Coil data (both real and imaginary).

    :param discretize.CylindricalMesh mesh: mesh used for the forward simulation
    :param numpy.ndarray dobs: observed data
    :param float src_height: height of the source above the ground
    :param numpy.ndarray freqs: frequencies
    :param numpy.ndarray m0: starting model
    :param numpy.ndarray mref: reference model
    :param maps.IdentityMap mapping: mapping that maps the model to electrical conductivity
    :param float relative: percent error used to construct the data misfit term
    :param float floor: noise floor used to construct the data misfit term
    :param float rxOffset: offset between source and receiver.
    """

    # ------------------- Forward Simulation ------------------- #
    # set up the receivers
    bzr = FDEM.Rx.PointMagneticFluxDensitySecondary(
        np.array([[rxOffset, 0.0, src_height]]), orientation="z", component="real"
    )

    bzi = FDEM.Rx.PointMagneticFluxDensity(
        np.array([[rxOffset, 0.0, src_height]]), orientation="z", component="imag"
    )

    # source location
    srcLoc = np.array([0.0, 0.0, src_height])
    source_list = [
        FDEM.Src.MagDipole([bzr, bzi], freq, srcLoc, orientation="Z") for freq in freqs
    ]

    # construct a forward simulation
    survey = FDEM.Survey(source_list)
    prb = FDEM.Simulation3DMagneticFluxDensity(
        mesh, sigmaMap=mapping, Solver=PardisoSolver
    )
    prb.survey = survey

    # ------------------- Inversion ------------------- #
    # data misfit term
    uncert = abs(dobs) * relative + floor
    dat = data.Data(dobs=dobs, standard_deviation=uncert)
    dmisfit = data_misfit.L2DataMisfit(simulation=prb, data=dat)

    # regularization
    regMesh = discretize.TensorMesh([mesh.h[2][mapping.maps[-1].indActive]])
    reg = regularization.WeightedLeastSquares(regMesh)
    reg.reference_model = mref

    # optimization
    opt = optimization.InexactGaussNewton(maxIter=10)

    # statement of the inverse problem
    invProb = inverse_problem.BaseInvProblem(dmisfit, reg, opt)

    # Inversion directives and parameters
    target = directives.TargetMisfit()
    inv = inversion.BaseInversion(invProb, directiveList=[target])

    invProb.beta = 2.0  # Fix beta in the nonlinear iterations
    reg.alpha_s = 1e-3
    reg.alpha_x = 1.0
    prb.counter = opt.counter = utils.Counter()
    opt.LSshorten = 0.5
    opt.remember("xc")

    # run the inversion
    mopt = inv.run(m0)
    return mopt, invProb.dpred, survey.dobs


def run(runIt=False, plotIt=True, saveIt=False, saveFig=False, cleanup=True):
    """
    Run the bookpurnong 1D stitched RESOLVE inversions.

    :param bool runIt: re-run the inversions? Default downloads and plots saved results
    :param bool plotIt: show the plots?
    :param bool saveIt: save the re-inverted results?
    :param bool saveFig: save the figure
    :param bool cleanup: remove the downloaded results
    """

    # download the data
    downloads, directory = download_and_unzip_data()

    # Load resolve data
    resolve = h5py.File(os.path.sep.join([directory, "booky_resolve.hdf5"]), "r")

    river_path = resolve["river_path"][()]  # River path
    nSounding = resolve["data"].shape[0]  # the # of soundings

    # Bird height from surface
    b_height_resolve = resolve["src_elevation"][()]

    # fetch the frequencies we are considering
    cpi_inds = [0, 2, 6, 8, 10]  # Indices for HCP in-phase
    cpq_inds = [1, 3, 7, 9, 11]  # Indices for HCP quadrature
    frequency_cp = resolve["frequency_cp"][()]

    # build a mesh
    cs, ncx, npad = 1.0, 10.0, 20
    hx = [(cs, ncx), (cs, npad, 1.3)]
    npad = 12
    temp = np.logspace(np.log10(1.0), np.log10(12.0), 19)
    temp_pad = temp[-1] * 1.3 ** np.arange(npad)
    hz = np.r_[temp_pad[::-1], temp[::-1], temp, temp_pad]
    mesh = discretize.CylindricalMesh([hx, 1, hz], "00C")
    active = mesh.cell_centers_z < 0.0

    # survey parameters
    rxOffset = 7.86  # tx-rx separation
    bp = -mu_0 / (4 * np.pi * rxOffset**3)  # primary magnetic field

    # re-run the inversion
    if runIt:
        # set up the mappings - we are inverting for 1D log conductivity
        # below the earth's surface.
        actMap = maps.InjectActiveCells(
            mesh, active, np.log(1e-8), nC=mesh.shape_cells[2]
        )
        mapping = maps.ExpMap(mesh) * maps.SurjectVertical1D(mesh) * actMap

        # build starting and reference model
        sig_half = 1e-1
        sig_air = 1e-8
        sigma = np.ones(mesh.shape_cells[2]) * sig_air
        sigma[active] = sig_half
        m0 = np.log(1e-1) * np.ones(active.sum())  # starting model
        mref = np.log(1e-1) * np.ones(active.sum())  # reference model

        # initalize empty lists for storing inversion results
        mopt_re = []  # recovered model
        dpred_re = []  # predicted data
        dobs_re = []  # observed data

        # set up a noise model
        # 10% for the 3 lowest frequencies, 15% for the two highest
        relative = np.repeat(np.r_[np.ones(3) * 0.1, np.ones(2) * 0.15], 2)
        floor = abs(20 * bp * 1e-6)  # floor of 20ppm

        # loop over the soundings and invert each
        for rxind in range(nSounding):
            # convert data from ppm to magnetic field (A/m^2)
            dobs = (
                np.c_[
                    resolve["data"][rxind, :][cpi_inds].astype(float),
                    resolve["data"][rxind, :][cpq_inds].astype(float),
                ].flatten()
                * bp
                * 1e-6
            )

            # perform the inversion
            src_height = b_height_resolve[rxind].astype(float)
            mopt, dpred, dobs = resolve_1Dinversions(
                mesh,
                dobs,
                src_height,
                frequency_cp,
                m0,
                mref,
                mapping,
                relative=relative,
                floor=floor,
            )

            # add results to our list
            mopt_re.append(mopt)
            dpred_re.append(dpred)
            dobs_re.append(dobs)

        # save results
        mopt_re = np.vstack(mopt_re)
        dpred_re = np.vstack(dpred_re)
        dobs_re = np.vstack(dobs_re)

        if saveIt:
            np.save("mopt_re_final", mopt_re)
            np.save("dobs_re_final", dobs_re)
            np.save("dpred_re_final", dpred_re)

    mopt_re = resolve["mopt"][()]
    dobs_re = resolve["dobs"][()]
    dpred_re = resolve["dpred"][()]

    sigma = np.exp(mopt_re)
    indz = -7  # depth index

    # so that we can visually compare with literature (eg Viezzoli, 2010)
    cmap = "jet"

    # dummy figure for colobar
    fig = plt.figure()
    out = plt.scatter(np.ones(3), np.ones(3), c=np.linspace(-2, 1, 3), cmap=cmap)
    plt.close(fig)

    # plot from the paper
    plt.figure(figsize=(13, 7))
    ax0 = plt.subplot2grid((2, 3), (0, 0), rowspan=2, colspan=2)
    ax1 = plt.subplot2grid((2, 3), (0, 2))
    ax2 = plt.subplot2grid((2, 3), (1, 2))

    # titles of plots
    title = [
        ("(a) Recovered model, %.1f m depth") % (-mesh.cell_centers_z[active][indz]),
        "(b) Obs (Real 400 Hz)",
        "(c) Pred (Real 400 Hz)",
    ]

    temp = sigma[:, indz]
    tree = cKDTree(list(zip(resolve["xy"][:, 0], resolve["xy"][:, 1])))
    d, d_inds = tree.query(list(zip(resolve["xy"][:, 0], resolve["xy"][:, 1])), k=20)
    w = 1.0 / (d + 100.0) ** 2.0
    w = utils.sdiag(1.0 / np.sum(w, axis=1)) * (w)
    xy = resolve["xy"]
    temp = (temp.flatten()[d_inds] * w).sum(axis=1)
    utils.plot2Ddata(
        xy,
        temp,
        ncontour=100,
        scale="log",
        dataloc=False,
        contourOpts={"cmap": cmap, "vmin": 1e-2, "vmax": 1e1},
        ax=ax0,
    )
    ax0.plot(resolve["xy"][:, 0], resolve["xy"][:, 1], "k.", alpha=0.02, ms=1)

    cb = plt.colorbar(out, ax=ax0, ticks=np.linspace(-2, 1, 4), format="$10^{%.1f}$")
    cb.set_ticklabels(["0.01", "0.1", "1", "10"])
    cb.set_label("Conductivity (S/m)")
    ax0.plot(river_path[:, 0], river_path[:, 1], "k-", lw=0.5)

    # plot observed and predicted data
    freq_ind = 0
    temp_dobs = dobs_re[:, freq_ind].copy()
    ax1.plot(river_path[:, 0], river_path[:, 1], "k-", lw=0.5)
    inf = temp_dobs / abs(bp) * 1e6
    print(inf.min(), inf.max())
    out = utils.plot2Ddata(
        resolve["xy"][()],
        temp_dobs / abs(bp) * 1e6,
        ncontour=100,
        scale="log",
        dataloc=False,
        ax=ax1,
        contourOpts={"cmap": "viridis"},
    )
    vmin, vmax = out[0].get_clim()
    print(vmin, vmax)
    cb = plt.colorbar(
        out[0],
        ticks=np.logspace(np.log10(vmin), np.log10(vmax), 3),
        ax=ax1,
        format="%.1e",
        fraction=0.046,
        pad=0.04,
    )
    cb.set_label("Bz (ppm)")
    temp_dpred = dpred_re[:, freq_ind].copy()
    # temp_dpred[mask_:_data] = np.nan
    ax2.plot(river_path[:, 0], river_path[:, 1], "k-", lw=0.5)
    utils.plot2Ddata(
        resolve["xy"][()],
        temp_dpred / abs(bp) * 1e6,
        ncontour=100,
        scale="log",
        dataloc=False,
        contourOpts={"vmin": vmin, "vmax": vmax, "cmap": "viridis"},
        ax=ax2,
    )
    cb = plt.colorbar(
        out[0],
        ticks=np.logspace(np.log10(vmin), np.log10(vmax), 3),
        ax=ax2,
        format="%.1e",
        fraction=0.046,
        pad=0.04,
    )
    cb.set_label("Bz (ppm)")

    for i, ax in enumerate([ax0, ax1, ax2]):
        xticks = [460000, 463000]
        yticks = [6195000, 6198000, 6201000]
        ax.set_xticks(xticks)
        ax.set_yticks(yticks)
        ax.plot(river_path[:, 0], river_path[:, 1], "k", lw=0.5)

        ax.set_aspect("equal")
        ax.plot(resolve["xy"][:, 0], resolve["xy"][:, 1], "k.", alpha=0.02, ms=1)

        ax.set_yticklabels([str(f) for f in yticks])
        ax.set_ylabel("Northing (m)")
        ax.set_xlabel("Easting (m)")
        ax.set_title(title[i])

    plt.tight_layout()

    if plotIt:
        plt.show()

    if saveFig is True:
        fig.savefig("obspred_resolve.png", dpi=200)

    resolve.close()
    if cleanup:
        os.remove(downloads)
        shutil.rmtree(directory)


if __name__ == "__main__":
    run(runIt=False, plotIt=True, saveIt=True, saveFig=False, cleanup=True)

Estimated memory usage: 8 MB