Time-domain CSEM for a resistive cube in a deep marine setting

import empymod
import discretize

try:
    from pymatsolver import Pardiso as Solver
except ImportError:
    from simpeg import SolverLU as Solver

import numpy as np
from simpeg import maps
from simpeg.electromagnetics import time_domain as TDEM
import matplotlib.pyplot as plt

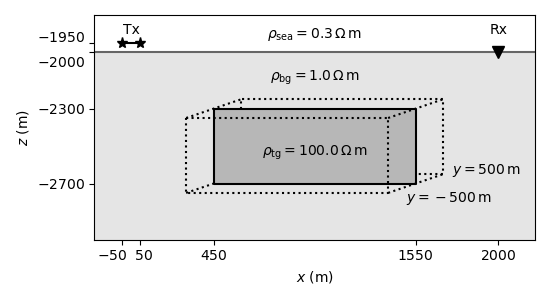
(A) Model

fig = plt.figure(figsize=(5.5, 3))
ax = plt.gca()

# Seafloor and background
plt.plot([-200, 2200], [-2000, -2000], "-", c=".4")
bg = plt.Rectangle((-500, -3000), 3000, 1000, facecolor="black", alpha=0.1)
ax.add_patch(bg)

# Plot survey
plt.plot([-50, 50], [-1950, -1950], "*-", ms=8, c="k")
plt.plot(2000, -2000, "v", ms=8, c="k")
plt.text(0, -1900, r"Tx", horizontalalignment="center")
plt.text(2000, -1900, r"Rx", horizontalalignment="center")

# Plot cube
plt.plot([450, 1550, 1550, 450, 450], [-2300, -2300, -2700, -2700, -2300], "k-")
plt.plot([300, 1400, 1400, 300, 300], [-2350, -2350, -2750, -2750, -2350], "k:")
plt.plot([600, 600, 1700, 1700, 1550], [-2300, -2250, -2250, -2650, -2650], "k:")
plt.plot([300, 600], [-2350, -2250], "k:")
plt.plot([1400, 1700], [-2350, -2250], "k:")
plt.plot([300, 450], [-2750, -2700], "k:")
plt.plot([1400, 1700], [-2750, -2650], "k:")
tg = plt.Rectangle((450, -2700), 1100, 400, facecolor="black", alpha=0.2)
ax.add_patch(tg)

# Annotate resistivities
plt.text(
    1000, -1925, r"$\rho_\mathrm{sea}=0.3\,\Omega\,$m", horizontalalignment="center"
)
plt.text(
    1000, -2150, r"$\rho_\mathrm{bg}=1.0\,\Omega\,$m", horizontalalignment="center"
)
plt.text(
    1000, -2550, r"$\rho_\mathrm{tg}=100.0\,\Omega\,$m", horizontalalignment="center"
)
plt.text(1500, -2800, r"$y=-500\,$m", horizontalalignment="left")
plt.text(1750, -2650, r"$y=500\,$m", horizontalalignment="left")

# Ticks and labels
plt.xticks(
    [-50, 50, 450, 1550, 2000],
    ["$-50~$ $~$  $~$", " $~50$", "$450$", "$1550$", "$2000$"],
)
plt.yticks(
    [-1950, -2000, -2300, -2700], ["$-1950$\n", "\n$-2000$", "$-2300$", "$-2700$"]
)

plt.xlim([-200, 2200])
plt.ylim([-3000, -1800])

plt.xlabel("$x$ (m)")
plt.ylabel("$z$ (m)")
plt.tight_layout()

plt.show()

# Resistivities
res_sea = 0.3
res_bg = 1.0
res_tg = 100.0

# Seafloor
seafloor = -2000

# Target dimension
tg_x = [450, 1550]
tg_y = [-500, 500]
tg_z = [-2700, -2300]

(B) Survey

# Source: 100 m x-directed diplole at the origin,
# 50 m above seafloor, src [x1, x2, y1, y2, z1, z2]
src = [-50, 50, 0, 0, -1950, -1950]

# Receiver: x-directed dipole at 2 km on the
# seafloor, rec = [x, y, z, azimuth, dip]
rec = [2000, 0, -2000, 0, 0]

# Times to compute, 0.1 - 10 s, 301 steps
times = np.logspace(-1, 1, 301)

(C) Modelling parameters

Check diffusion distances

# Get min/max diffusion distances for the two halfspaces.
diff_dist0 = 1261 * np.sqrt(np.r_[times * res_sea, times * res_sea])
diff_dist1 = 1261 * np.sqrt(np.r_[times * res_bg, times * res_bg])
diff_dist2 = 1261 * np.sqrt(np.r_[times * res_tg, times * res_tg])
print("Min/max diffusion distance:")
print(f"- Water      :: {diff_dist0.min():8.0f} / {diff_dist0.max():8.0f} m.")
print(f"- Background :: {diff_dist1.min():8.0f} / {diff_dist1.max():8.0f} m.")
print(f"- Target     :: {diff_dist2.min():8.0f} / {diff_dist2.max():8.0f} m.")

Min/max diffusion distance:
- Water      ::      218 /     2184 m.
- Background ::      399 /     3988 m.
- Target     ::     3988 /    39876 m.

Time-steps

# Time steps
time_steps = [1e-1, (1e-2, 21), (3e-2, 23), (1e-1, 21), (3e-1, 23)]

# Create mesh with time steps
ts = discretize.TensorMesh([time_steps]).nodes_x

# Plot them
plt.figure(figsize=(9, 1.5))

# Logarithmic scale
plt.subplot(121)
plt.title("Check time-steps on logarithmic-scale")
plt.plot([times.min(), times.min()], [-1, 1])
plt.plot([times.max(), times.max()], [-1, 1])
plt.plot(ts, ts * 0, ".", ms=2)
plt.yticks([])
plt.xscale("log")
plt.xlabel("Time (s)")

# Linear scale
plt.subplot(122)
plt.title("Check time-steps on linear-scale")
plt.plot([times.min(), times.min()], [-1, 1])
plt.plot([times.max(), times.max()], [-1, 1])
plt.plot(ts, ts * 0, ".", ms=2)
plt.yticks([])
plt.xlabel("Time (s)")

plt.tight_layout()
plt.show()

# Check times with time-steps
print(f"Min/max times    : {times.min():.1e} / {times.max():.1e}")
print(f"Min/max timeSteps: {ts[1]:.1e} / {ts[-1]:.1e}")

Min/max times    : 1.0e-01 / 1.0e+01
Min/max timeSteps: 1.0e-01 / 1.0e+01

Create mesh (discretize)

# Cell width, number of cells
width = 100
nx = rec[0] // width + 4
ny = 10
nz = 9

# Padding
npadx = 14
npadyz = 12

# Stretching
alpha = 1.3

# Initiate TensorMesh
mesh = discretize.TensorMesh(
    [
        [(width, npadx, -alpha), (width, nx), (width, npadx, alpha)],
        [(width, npadyz, -alpha), (width, ny), (width, npadyz, alpha)],
        [(width, npadyz, -alpha), (width, nz), (width, npadyz, alpha)],
    ],
    x0="CCC",
)

# Shift mesh so that
# x=0 is at midpoint of source;
# z=-2000 is at receiver level
mesh.x0[0] += rec[0] // 2 - width / 2
mesh.x0[2] -= nz / 2 * width - seafloor
mesh

TensorMesh			58,344 cells
		MESH EXTENT		CELL WIDTH		FACTOR
dir	nC	min	max	min	max	max
x	52	-16,878.63	18,778.63	100.00	3,937.38	1.30
y	34	-10,162.50	10,162.50	100.00	2,329.81	1.30
z	33	-12,562.50	7,662.50	100.00	2,329.81	1.30

Check if source and receiver are exactly at x-edges.

No requirement; if receiver are exactly on x-edges then no interpolation is required to get the responses (cell centers in x, cell edges in y, z).

print(
    f"Rec-{{x;y;z}} :: {rec[0] in np.round(mesh.cell_centers_x)!s:>5}; "
    f"{rec[1] in np.round(mesh.nodes_y)!s:>5}; "
    f"{rec[2] in np.round(mesh.nodes_z)!s:>5}"
)
print(
    f"Src-x       :: {src[0] in np.round(mesh.cell_centers_x)!s:>5}; "
    f"{src[1] in np.round(mesh.cell_centers_x)!s:>5}"
)
print(
    f"Src-y       :: {src[2] in np.round(mesh.nodes_y)!s:>5}; "
    f"{src[3] in np.round(mesh.nodes_y)!s:>5}"
)
print(
    f"Src-z       :: {src[4] in np.round(mesh.nodes_z)!s:>5}; "
    f"{src[5] in np.round(mesh.nodes_z)!s:>5}"
)

Rec-{x;y;z} ::  True;  True;  True
Src-x       :: False; False
Src-y       ::  True;  True
Src-z       :: False; False

Put model on mesh

# Background model
mres_bg = np.ones(mesh.nC) * res_sea  # Upper halfspace; sea water
mres_bg[mesh.gridCC[:, 2] < seafloor] = res_bg  # Lower halfspace; background

# Target model
mres_tg = mres_bg.copy()  # Copy background model
target_inds = (  # Find target indices
    (mesh.gridCC[:, 0] >= tg_x[0])
    & (mesh.gridCC[:, 0] <= tg_x[1])
    & (mesh.gridCC[:, 1] >= tg_y[0])
    & (mesh.gridCC[:, 1] <= tg_y[1])
    & (mesh.gridCC[:, 2] >= tg_z[0])
    & (mesh.gridCC[:, 2] <= tg_z[1])
)
mres_tg[target_inds] = res_tg  # Target resistivity

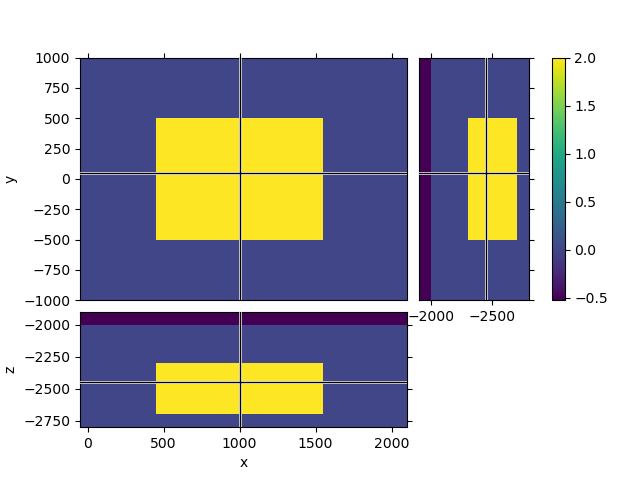
# QC
mesh.plot_3d_slicer(
    np.log10(mres_tg),
    clim=[np.log10(res_sea), np.log10(res_tg)],
    xlim=[-src[0] - 100, rec[0] + 100],
    ylim=[-rec[0] / 2, rec[0] / 2],
    zlim=[tg_z[0] - 100, seafloor + 100],
)

(D) empymod

Compute the 1D background semi-analytically, using 5 points to approximate the 100-m long dipole.

inp = {
    "src": src.copy(),
    "rec": rec.copy(),
    "depth": seafloor,
    "res": [res_sea, res_bg],
    "freqtime": times,
    "signal": -1,  # Switch-off
    "srcpts": 5,  # 5 points for finite length approx
    "strength": 1,  # Account for source length
    "verb": 1,
}

epm_bg = empymod.bipole(**inp)

(E) simpeg

Set-up simpeg-specific parameters.

# Set up the receiver list
rec_list = [
    TDEM.Rx.PointElectricField(
        orientation="x",
        times=times,
        locations=np.array(
            [
                [*rec[:3]],
            ]
        ),
    ),
]


# Set up the source list
src_list = [
    TDEM.Src.LineCurrent(
        receiver_list=rec_list,
        location=np.array([[*src[::2]], [*src[1::2]]]),
    ),
]


# Create `Survey`
survey = TDEM.Survey(src_list)


# Define the `Simulation`
prob = TDEM.Simulation3DElectricField(
    mesh,
    survey=survey,
    rhoMap=maps.IdentityMap(mesh),
    solver=Solver,
    time_steps=time_steps,
)

Compute

spg_bg = prob.dpred(mres_bg)
spg_tg = prob.dpred(mres_tg)

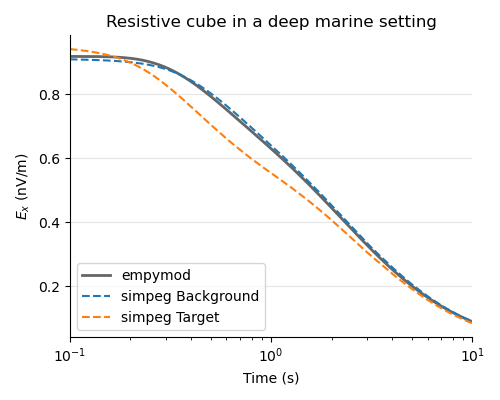
(F) Plots

plt.figure(figsize=(5, 4))
ax1 = plt.subplot(111)

plt.title("Resistive cube in a deep marine setting")

plt.plot(times, epm_bg * 1e9, ".4", lw=2, label="empymod")

plt.plot(times, spg_bg * 1e9, "C0--", label="simpeg Background")
plt.plot(times, spg_tg * 1e9, "C1--", label="simpeg Target")

plt.ylabel("$E_x$ (nV/m)")
plt.xscale("log")
plt.xlim([0.1, 10])
plt.legend(loc=3)
plt.grid(axis="y", c="0.9")

plt.xlabel("Time (s)")

# Switch off spines
ax1.spines["top"].set_visible(False)
ax1.spines["right"].set_visible(False)

plt.tight_layout()
plt.show()

empymod.Report([simpeg, discretize, pymatsolver])

Estimated memory usage: 1984 MB