Note
Go to the end to download the full example code.
Sparse Inversion with Iteratively Re-Weighted Least-Squares#
Least-squares inversion produces smooth models which may not be an accurate representation of the true model. Here we demonstrate the basics of inverting for sparse and/or blocky models. Here, we used the iteratively reweighted least-squares approach. For this tutorial, we focus on the following:
Defining the forward problem
Defining the inverse problem (data misfit, regularization, optimization)
Defining the paramters for the IRLS algorithm
Specifying directives for the inversion
Recovering a set of model parameters which explains the observations
import numpy as np
import matplotlib.pyplot as plt
from discretize import TensorMesh
from simpeg import (
simulation,
maps,
data_misfit,
directives,
optimization,
regularization,
inverse_problem,
inversion,
)
# sphinx_gallery_thumbnail_number = 3
Defining the Model and Mapping#
Here we generate a synthetic model and a mappig which goes from the model space to the row space of our linear operator.
nParam = 100 # Number of model paramters
# A 1D mesh is used to define the row-space of the linear operator.
mesh = TensorMesh([nParam])
# Creating the true model
true_model = np.zeros(mesh.nC)
true_model[mesh.cell_centers_x > 0.3] = 1.0
true_model[mesh.cell_centers_x > 0.45] = -0.5
true_model[mesh.cell_centers_x > 0.6] = 0
# Mapping from the model space to the row space of the linear operator
model_map = maps.IdentityMap(mesh)
# Plotting the true model
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(111)
ax.plot(mesh.cell_centers_x, true_model, "b-")
ax.set_ylim([-2, 2])
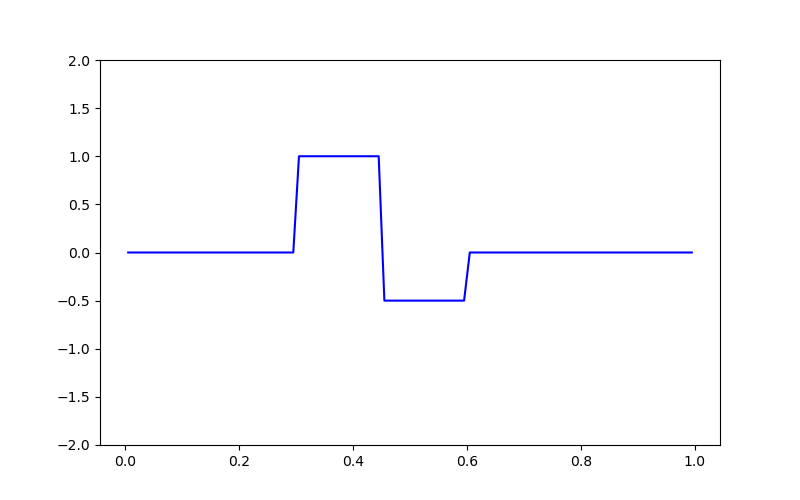
(-2.0, 2.0)
Defining the Linear Operator#
Here we define the linear operator with dimensions (nData, nParam). In practive, you may have a problem-specific linear operator which you would like to construct or load here.
# Number of data observations (rows)
nData = 20
# Create the linear operator for the tutorial. The columns of the linear operator
# represents a set of decaying and oscillating functions.
jk = np.linspace(1.0, 60.0, nData)
p = -0.25
q = 0.25
def g(k):
return np.exp(p * jk[k] * mesh.cell_centers_x) * np.cos(
np.pi * q * jk[k] * mesh.cell_centers_x
)
G = np.empty((nData, nParam))
for i in range(nData):
G[i, :] = g(i)
# Plot the columns of G
fig = plt.figure(figsize=(8, 5))
ax = fig.add_subplot(111)
for i in range(G.shape[0]):
ax.plot(G[i, :])
ax.set_title("Columns of matrix G")
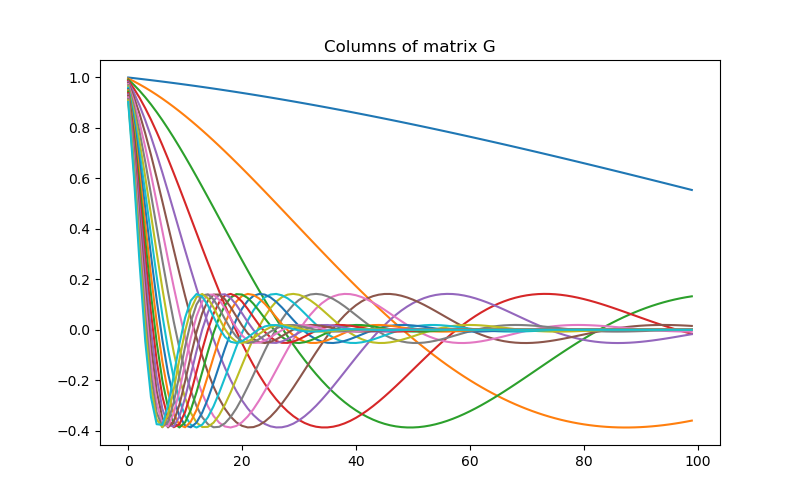
Text(0.5, 1.0, 'Columns of matrix G')
Defining the Simulation#
The simulation defines the relationship between the model parameters and predicted data.
Predict Synthetic Data#
Here, we use the true model to create synthetic data which we will subsequently invert.
# Standard deviation of Gaussian noise being added
std = 0.02
np.random.seed(1)
# Create a SimPEG data object
data_obj = sim.make_synthetic_data(true_model, noise_floor=std, add_noise=True)
Define the Inverse Problem#
The inverse problem is defined by 3 things:
Data Misfit: a measure of how well our recovered model explains the field data
Regularization: constraints placed on the recovered model and a priori information
Optimization: the numerical approach used to solve the inverse problem
# Define the data misfit. Here the data misfit is the L2 norm of the weighted
# residual between the observed data and the data predicted for a given model.
# Within the data misfit, the residual between predicted and observed data are
# normalized by the data's standard deviation.
dmis = data_misfit.L2DataMisfit(simulation=sim, data=data_obj)
# Define the regularization (model objective function). Here, 'p' defines the
# the norm of the smallness term and 'q' defines the norm of the smoothness
# term.
reg = regularization.Sparse(mesh, mapping=model_map)
reg.reference_model = np.zeros(nParam)
p = 0.0
q = 0.0
reg.norms = [p, q]
# Define how the optimization problem is solved.
opt = optimization.ProjectedGNCG(
maxIter=100, lower=-2.0, upper=2.0, maxIterLS=20, cg_maxiter=30, cg_rtol=1e-3
)
# Here we define the inverse problem that is to be solved
inv_prob = inverse_problem.BaseInvProblem(dmis, reg, opt)
Define Inversion Directives#
Here we define any directiveas that are carried out during the inversion. This includes the cooling schedule for the trade-off parameter (beta), stopping criteria for the inversion and saving inversion results at each iteration.
# Add sensitivity weights but don't update at each beta
sensitivity_weights = directives.UpdateSensitivityWeights(every_iteration=False)
# Reach target misfit for L2 solution, then use IRLS until model stops changing.
IRLS = directives.UpdateIRLS(max_irls_iterations=40, f_min_change=1e-4)
# Defining a starting value for the trade-off parameter (beta) between the data
# misfit and the regularization.
starting_beta = directives.BetaEstimate_ByEig(beta0_ratio=1e0)
# Update the preconditionner
update_Jacobi = directives.UpdatePreconditioner()
# Save output at each iteration
saveDict = directives.SaveOutputEveryIteration(save_txt=False)
# Define the directives as a list
directives_list = [
sensitivity_weights,
IRLS,
starting_beta,
update_Jacobi,
saveDict,
]
/home/vsts/work/1/s/simpeg/directives/_directives.py:1865: FutureWarning:
SaveEveryIteration.save_txt has been deprecated, please use SaveEveryIteration.on_disk. It will be removed in version 0.26.0 of SimPEG.
/home/vsts/work/1/s/simpeg/directives/_directives.py:1866: FutureWarning:
SaveEveryIteration.save_txt has been deprecated, please use SaveEveryIteration.on_disk. It will be removed in version 0.26.0 of SimPEG.
Setting a Starting Model and Running the Inversion#
To define the inversion object, we need to define the inversion problem and the set of directives. We can then run the inversion.
# Here we combine the inverse problem and the set of directives
inv = inversion.BaseInversion(inv_prob, directives_list)
# Starting model
starting_model = 1e-4 * np.ones(nParam)
# Run inversion
recovered_model = inv.run(starting_model)
Running inversion with SimPEG v0.25.1.dev1+g9a8c46e88
================================================= Projected GNCG =================================================
# beta phi_d phi_m f |proj(x-g)-x| LS iter_CG CG |Ax-b|/|b| CG |Ax-b| Comment
-----------------------------------------------------------------------------------------------------------------
0 1.73e+06 3.69e+03 1.03e-09 3.69e+03 0 inf inf
1 1.73e+06 1.89e+03 3.64e-04 2.52e+03 1.95e+01 0 8 2.96e-04 1.54e+00
2 8.66e+05 1.31e+03 8.48e-04 2.04e+03 1.90e+01 0 9 3.55e-04 2.94e-01
3 4.33e+05 7.72e+02 1.73e-03 1.52e+03 1.87e+01 0 9 8.47e-04 5.13e-01
4 2.17e+05 3.86e+02 2.98e-03 1.03e+03 1.75e+01 0 10 8.39e-04 3.58e-01
5 1.08e+05 1.68e+02 4.38e-03 6.41e+02 1.70e+01 0 13 5.51e-04 1.53e-01
6 5.41e+04 6.62e+01 5.66e-03 3.73e+02 1.53e+01 0 12 9.30e-04 1.56e-01
7 2.71e+04 2.59e+01 6.68e-03 2.07e+02 1.34e+01 0 22 3.62e-04 3.43e-02
8 1.35e+04 1.17e+01 7.39e-03 1.12e+02 1.16e+01 0 29 6.34e-04 3.26e-02
Reached starting chifact with l2-norm regularization: Start IRLS steps...
irls_threshold 1.2141465314060733
9 1.35e+04 1.98e+01 9.15e-03 1.44e+02 1.59e+01 0 29 8.64e-04 2.85e-02
10 1.35e+04 2.69e+01 1.01e-02 1.63e+02 1.44e+01 0 22 9.18e-04 2.08e-02
11 1.01e+04 2.61e+01 1.13e-02 1.40e+02 2.99e+00 0 29 4.24e-04 5.32e-03
12 7.67e+03 2.46e+01 1.23e-02 1.19e+02 4.65e+00 0 27 8.26e-04 9.00e-03
13 5.99e+03 2.27e+01 1.31e-02 1.01e+02 5.12e+00 0 27 6.50e-04 6.29e-03
14 4.89e+03 2.05e+01 1.34e-02 8.58e+01 5.09e+00 0 24 5.93e-04 5.31e-03
15 4.89e+03 2.07e+01 1.26e-02 8.21e+01 7.88e+00 0 26 5.39e-04 4.55e-03
16 4.89e+03 2.07e+01 1.17e-02 7.77e+01 8.28e+00 0 23 9.90e-04 8.93e-03
17 4.89e+03 2.04e+01 1.06e-02 7.24e+01 8.58e+00 0 23 2.12e-04 2.01e-03
18 4.89e+03 1.99e+01 9.55e-03 6.65e+01 9.08e+00 0 22 7.92e-04 7.97e-03
19 4.89e+03 1.89e+01 8.43e-03 6.01e+01 9.30e+00 0 21 6.00e-04 6.36e-03
20 4.89e+03 1.78e+01 7.44e-03 5.42e+01 9.75e+00 0 23 2.71e-04 3.10e-03
21 7.63e+03 2.13e+01 5.76e-03 6.53e+01 1.64e+01 0 17 8.73e-04 3.84e-02
22 7.63e+03 2.15e+01 5.11e-03 6.05e+01 1.19e+01 0 18 9.87e-04 1.62e-02
23 7.63e+03 2.13e+01 4.56e-03 5.60e+01 1.23e+01 0 19 9.48e-04 1.77e-02
24 7.63e+03 2.11e+01 4.16e-03 5.28e+01 1.29e+01 0 19 9.13e-04 2.28e-02
25 7.63e+03 2.13e+01 3.77e-03 5.00e+01 1.32e+01 1 19 7.23e-04 2.18e-02
26 7.63e+03 2.12e+01 3.26e-03 4.60e+01 1.81e+01 0 17 5.81e-04 4.13e-02
27 7.63e+03 2.05e+01 2.78e-03 4.17e+01 1.20e+01 0 18 9.48e-04 2.35e-02
28 7.63e+03 1.96e+01 2.35e-03 3.76e+01 1.19e+01 0 19 9.56e-04 2.24e-02
29 7.63e+03 1.88e+01 1.97e-03 3.38e+01 1.17e+01 0 22 4.56e-04 1.02e-02
30 7.63e+03 1.84e+01 1.64e-03 3.09e+01 1.21e+01 1 25 9.91e-04 2.57e-02
31 7.63e+03 1.85e+01 1.37e-03 2.89e+01 1.30e+01 0 24 6.71e-04 2.92e-02
32 7.63e+03 1.84e+01 1.16e-03 2.73e+01 1.28e+01 0 26 9.66e-04 3.56e-02
33 7.63e+03 1.84e+01 9.94e-04 2.60e+01 1.22e+01 0 30 1.36e-03 3.65e-02
34 7.63e+03 1.83e+01 8.47e-04 2.48e+01 1.24e+01 0 30 2.34e-03 6.73e-02
35 7.63e+03 1.83e+01 7.18e-04 2.38e+01 1.22e+01 0 30 1.00e-02 3.05e-01
36 7.63e+03 1.83e+01 6.17e-04 2.31e+01 1.21e+01 1 30 5.68e-03 1.86e-01
37 7.63e+03 1.85e+01 5.17e-04 2.25e+01 1.42e+01 0 30 3.28e-03 2.01e-01
38 7.63e+03 1.87e+01 4.37e-04 2.20e+01 1.20e+01 0 30 9.96e-03 3.77e-01
39 7.63e+03 1.88e+01 3.70e-04 2.16e+01 1.17e+01 0 30 4.12e-03 1.55e-01
40 7.63e+03 1.89e+01 3.13e-04 2.13e+01 1.16e+01 0 30 1.98e-03 7.69e-02
41 7.63e+03 1.91e+01 2.66e-04 2.11e+01 1.15e+01 0 30 1.74e-02 6.92e-01
42 7.63e+03 1.91e+01 2.37e-04 2.09e+01 1.15e+01 2 30 5.17e-03 2.10e-01
43 7.63e+03 1.91e+01 2.19e-04 2.07e+01 1.25e+01 4 30 4.19e-03 2.73e-01
44 7.63e+03 1.93e+01 1.69e-04 2.06e+01 1.34e+01 0 24 7.27e-04 6.60e-02
45 7.63e+03 1.93e+01 1.47e-04 2.04e+01 1.16e+01 0 30 1.62e-03 9.72e-02
46 7.63e+03 1.92e+01 1.38e-04 2.02e+01 1.14e+01 0 30 4.81e-03 2.41e-01
47 7.63e+03 1.89e+01 1.23e-04 1.98e+01 1.14e+01 0 30 4.58e-03 2.15e-01
48 7.63e+03 1.85e+01 1.07e-04 1.93e+01 1.13e+01 0 30 1.33e-01 5.99e+00
Reach maximum number of IRLS cycles: 40
------------------------- STOP! -------------------------
1 : |fc-fOld| = 2.3051e-01 <= tolF*(1+|f0|) = 3.6935e+02
0 : |xc-x_last| = 1.0563e+00 <= tolX*(1+|x0|) = 1.0010e-01
0 : |proj(x-g)-x| = 1.1292e+01 <= tolG = 1.0000e-01
0 : |proj(x-g)-x| = 1.1292e+01 <= 1e3*eps = 1.0000e-02
0 : maxIter = 100 <= iter = 48
------------------------- DONE! -------------------------
Plotting Results#
fig, ax = plt.subplots(1, 2, figsize=(12 * 1.2, 4 * 1.2))
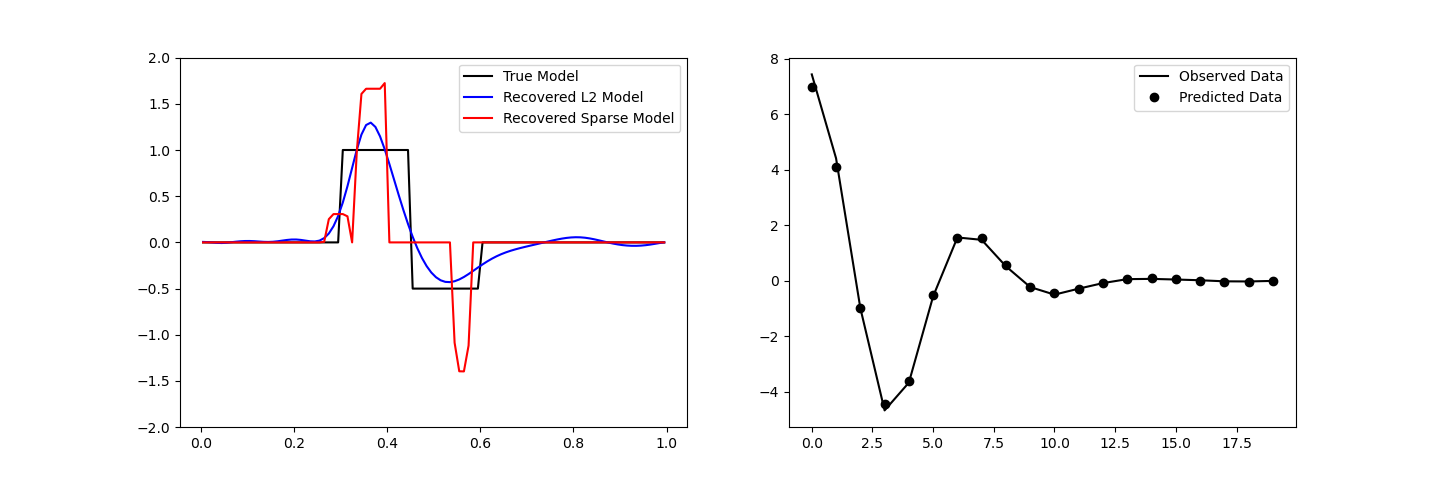
# True versus recovered model
ax[0].plot(mesh.cell_centers_x, true_model, "k-")
ax[0].plot(mesh.cell_centers_x, inv_prob.l2model, "b-")
ax[0].plot(mesh.cell_centers_x, recovered_model, "r-")
ax[0].legend(("True Model", "Recovered L2 Model", "Recovered Sparse Model"))
ax[0].set_ylim([-2, 2])
# Observed versus predicted data
ax[1].plot(data_obj.dobs, "k-")
ax[1].plot(inv_prob.dpred, "ko")
ax[1].legend(("Observed Data", "Predicted Data"))
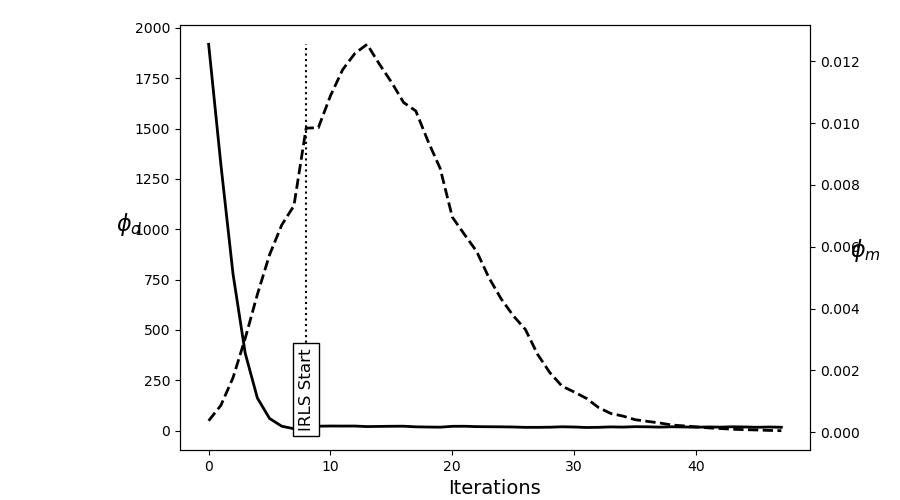
# Plot convergence
fig = plt.figure(figsize=(9, 5))
ax = fig.add_axes([0.2, 0.1, 0.7, 0.85])
ax.plot(saveDict.phi_d, "k", lw=2)
twin = ax.twinx()
twin.plot(saveDict.phi_m, "k--", lw=2)
ax.plot(
np.r_[IRLS.metrics.start_irls_iter, IRLS.metrics.start_irls_iter],
np.r_[0, np.max(saveDict.phi_d)],
"k:",
)
ax.text(
IRLS.metrics.start_irls_iter,
0.0,
"IRLS Start",
va="bottom",
ha="center",
rotation="vertical",
size=12,
bbox={"facecolor": "white"},
)
ax.set_ylabel(r"$\phi_d$", size=16, rotation=0)
ax.set_xlabel("Iterations", size=14)
twin.set_ylabel(r"$\phi_m$", size=16, rotation=0)
Text(865.1527777777777, 0.5, '$\\phi_m$')
Total running time of the script: (0 minutes 41.345 seconds)
Estimated memory usage: 321 MB