simpeg.electromagnetics.analytics.hzAnalyticDipoleF

simpeg.electromagnetics.analytics.hzAnalyticDipoleF(r, freq, sigma, secondary=True, mu=1.25663706212e-06)

The analytical expression is given in Equation 4.56 in Ward and Hohmann, 1988, and the example reproduces their Figure 4.2.

Examples

>>> import matplotlib.pyplot as plt
>>> from simpeg import electromagnetics as em
>>> freq = np.logspace(-1, 5, 301)
>>> test = em.analytics.hzAnalyticDipoleF(
>>>        100, freq, 0.01, secondary=False)
>>> plt.loglog(freq, test.real, 'C0-', label='Real')
>>> plt.loglog(freq, -test.real, 'C0--')
>>> plt.loglog(freq, test.imag, 'C1-', label='Imaginary')
>>> plt.loglog(freq, -test.imag, 'C1--')
>>> plt.title('Response at $r=100$ m')
>>> plt.xlim([1e-1, 1e5])
>>> plt.ylim([1e-12, 1e-6])
>>> plt.xlabel('Frequency (Hz)')
>>> plt.ylabel('$H_z$ (A/m)')
>>> plt.legend(loc=6)
>>> plt.show()

(Source code, png, pdf)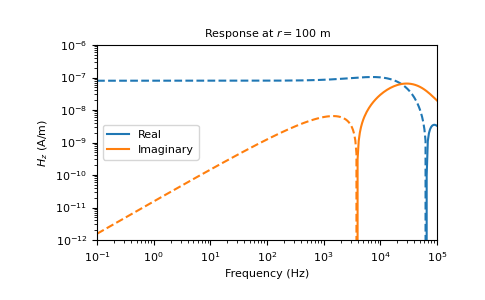

Reference

• Ward, S. H., and G. W. Hohmann, 1988, Electromagnetic theory for geophysical applications, Chapter 4 of Electromagnetic Methods in Applied Geophysics: SEG, Investigations in Geophysics No. 3, 130–311; DOI: 10.1190/1.9781560802631.ch4.