SimPEG.electromagnetics.time_domain.Simulation3DElectricField

class SimPEG.electromagnetics.time_domain.Simulation3DElectricField(mesh, survey=None, dt_threshold=1e-08, **kwargs)

Bases: BaseTDEMSimulation

Solve the EB-formulation of Maxwell’s equations for the electric field, e.

Starting with

\[\nabla \times \mathbf{e} + \frac{\partial \mathbf{b}}{\partial t} = \mathbf{s_m} \ \nabla \times \mu^{-1} \mathbf{b} - \sigma \mathbf{e} = \mathbf{s_e}\]

we eliminate \(\frac{\partial b}{\partial t}\) using

\[\frac{\partial \mathbf{b}}{\partial t} = - \nabla \times \mathbf{e} + \mathbf{s_m}\]

taking the time-derivative of Ampere’s law, we see

\[\frac{\partial}{\partial t}\left( \nabla \times \mu^{-1} \mathbf{b} - \sigma \mathbf{e} \right) = \frac{\partial \mathbf{s_e}}{\partial t} \ \nabla \times \mu^{-1} \frac{\partial \mathbf{b}}{\partial t} - \sigma \frac{\partial\mathbf{e}}{\partial t} = \frac{\partial \mathbf{s_e}}{\partial t}\]

which gives us

\[\nabla \times \mu^{-1} \nabla \times \mathbf{e} + \sigma \frac{\partial\mathbf{e}}{\partial t} = \nabla \times \mu^{-1} \mathbf{s_m} + \frac{\partial \mathbf{s_e}}{\partial t}\]

Attributes

Mcc	Cell center inner product matrix.
MccMu	Cell center property inner product matrix.
MccMuI	Cell center property inner product inverse matrix.
MccMui	Cell center property inner product matrix.
MccMuiI	Cell center property inner product inverse matrix.
MccRho	Cell center property inner product matrix.
MccRhoI	Cell center property inner product inverse matrix.
MccSigma	Cell center property inner product matrix.
MccSigmaI	Cell center property inner product inverse matrix.
Me	Edge inner product matrix.
MeI	Edge inner product inverse matrix.
MeMu	Edge property inner product matrix.
MeMuI	Edge property inner product inverse matrix.
MeMui	Edge property inner product matrix.
MeMuiI	Edge property inner product inverse matrix.
MeRho	Edge property inner product matrix.
MeRhoI	Edge property inner product inverse matrix.
MeSigma	Edge property inner product matrix.
MeSigmaI	Edge property inner product inverse matrix.
Mf	Face inner product matrix.
MfI	Face inner product inverse matrix.
MfMu	Face property inner product matrix.
MfMuI	Face property inner product inverse matrix.
MfMui	Face property inner product matrix.
MfMuiI	Face property inner product inverse matrix.
MfRho	Face property inner product matrix.
MfRhoI	Face property inner product inverse matrix.
MfSigma	Face property inner product matrix.
MfSigmaI	Face property inner product inverse matrix.
Mn	Node inner product matrix.
MnI	Node inner product inverse matrix.
MnMu	Node property inner product matrix.
MnMuI	Node property inner product inverse matrix.
MnMui	Node property inner product matrix.
MnMuiI	Node property inner product inverse matrix.
MnRho	Node property inner product matrix.
MnRhoI	Node property inner product inverse matrix.
MnSigma	Node property inner product matrix.
MnSigmaI	Node property inner product inverse matrix.
clean_on_model_update	A list of solver objects to clean when the model is updated
counter	SimPEG Counter object to store iterations and run-times.
deleteTheseOnModelUpdate	matrices to be deleted if the model for conductivity/resistivity is updated
dt_threshold	The threshold used to determine if a previous matrix factor can be reused.
mesh	Mesh for the simulation.
model	The inversion model.
mu	Magnetic permeability (h/m) physical property model.
muDeriv	Derivative of Magnetic Permeability (H/m) wrt the model.
muMap	Mapping of the inversion model to Magnetic Permeability (H/m).
mui	Inverse magnetic permeability (m/h) physical property model.
muiDeriv	Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
muiMap	Mapping of the inversion model to Inverse Magnetic Permeability (m/H).
nT	Total number of time steps.
needs_model	True if a model is necessary
rho	Electrical resistivity (ohm m) physical property model.
rhoDeriv	Derivative of Electrical resistivity (Ohm m) wrt the model.
rhoMap	Mapping of the inversion model to Electrical resistivity (Ohm m).
sensitivity_path	Path to directory where sensitivity file is stored.
sigma	Electrical conductivity (s/m) physical property model.
sigmaDeriv	Derivative of Electrical conductivity (S/m) wrt the model.
sigmaMap	Mapping of the inversion model to Electrical conductivity (S/m).
solver	Numerical solver used in the forward simulation.
solver_opts	Solver-specific parameters.
storeInnerProduct	Whether to store inner product matrices
survey	The survey for the simulation Returns ------- SimPEG.electromagnetics.time_domain.survey.Survey
t0	Initial time, in seconds, for the time-dependent forward simulation.
time_mesh	Time mesh for easy interpolation to observation times.
time_steps	Time step lengths, in seconds, for the time domain simulation.
times	Evaluation times.
verbose	Verbose progress printout.

Adcinv
MccI
Vol

Methods

Fields_Derivs	alias of FieldsDerivativesEB
Jtvec(m, v[, f])	Jvec computes the adjoint of the sensitivity times a vector
Jtvec_approx(m, v[, f])	Approximation of the Jacobian transpose times a vector for the model provided.
Jvec(m, v[, f])	Jvec computes the sensitivity times a vector
Jvec_approx(m, v[, f])	Approximation of the Jacobian times a vector for the model provided.
MccMuDeriv(u[, v, adjoint])	Derivative of MccProperty with respect to the model.
MccMuIDeriv(u[, v, adjoint])	Derivative of MccPropertyI with respect to the model.
MccMuiDeriv(u[, v, adjoint])	Derivative of MccProperty with respect to the model.
MccMuiIDeriv(u[, v, adjoint])	Derivative of MccPropertyI with respect to the model.
MccRhoDeriv(u[, v, adjoint])	Derivative of MccProperty with respect to the model.
MccRhoIDeriv(u[, v, adjoint])	Derivative of MccPropertyI with respect to the model.
MccSigmaDeriv(u[, v, adjoint])	Derivative of MccProperty with respect to the model.
MccSigmaIDeriv(u[, v, adjoint])	Derivative of MccPropertyI with respect to the model.
MeMuDeriv(u[, v, adjoint])	Derivative of MeProperty with respect to the model.
MeMuIDeriv(u[, v, adjoint])	Derivative of MePropertyI with respect to the model.
MeMuiDeriv(u[, v, adjoint])	Derivative of MeProperty with respect to the model.
MeMuiIDeriv(u[, v, adjoint])	Derivative of MePropertyI with respect to the model.
MeRhoDeriv(u[, v, adjoint])	Derivative of MeProperty with respect to the model.
MeRhoIDeriv(u[, v, adjoint])	Derivative of MePropertyI with respect to the model.
MeSigmaDeriv(u[, v, adjoint])	Derivative of MeProperty with respect to the model.
MeSigmaIDeriv(u[, v, adjoint])	Derivative of MePropertyI with respect to the model.
MfMuDeriv(u[, v, adjoint])	Derivative of MfProperty with respect to the model.
MfMuIDeriv(u[, v, adjoint])	I Derivative of MfPropertyI with respect to the model.
MfMuiDeriv(u[, v, adjoint])	Derivative of MfProperty with respect to the model.
MfMuiIDeriv(u[, v, adjoint])	I Derivative of MfPropertyI with respect to the model.
MfRhoDeriv(u[, v, adjoint])	Derivative of MfProperty with respect to the model.
MfRhoIDeriv(u[, v, adjoint])	I Derivative of MfPropertyI with respect to the model.
MfSigmaDeriv(u[, v, adjoint])	Derivative of MfProperty with respect to the model.
MfSigmaIDeriv(u[, v, adjoint])	I Derivative of MfPropertyI with respect to the model.
MnMuDeriv(u[, v, adjoint])	Derivative of MnProperty with respect to the model.
MnMuIDeriv(u[, v, adjoint])	Derivative of MnPropertyI with respect to the model.
MnMuiDeriv(u[, v, adjoint])	Derivative of MnProperty with respect to the model.
MnMuiIDeriv(u[, v, adjoint])	Derivative of MnPropertyI with respect to the model.
MnRhoDeriv(u[, v, adjoint])	Derivative of MnProperty with respect to the model.
MnRhoIDeriv(u[, v, adjoint])	Derivative of MnPropertyI with respect to the model.
MnSigmaDeriv(u[, v, adjoint])	Derivative of MnProperty with respect to the model.
MnSigmaIDeriv(u[, v, adjoint])	Derivative of MnPropertyI with respect to the model.
dpred([m, f])	Predicted data for the model provided.
fields(m)	Solve the forward problem for the fields.
fieldsPair	alias of Fields3DElectricField
getAdiag(tInd)	Diagonal of the system matrix at a given time index
getAdiagDeriv(tInd, u, v[, adjoint])	Deriv of ADiag with respect to electrical conductivity
getAsubdiag(tInd)	Matrix below the diagonal
getAsubdiagDeriv(tInd, u, v[, adjoint])	Derivative of the matrix below the diagonal with respect to electrical conductivity
getInitialFields()	Ask the sources for initial fields
getRHS(tInd)	right hand side
getSourceTerm(tInd)	Assemble the source term.
make_synthetic_data(m[, relative_error, ...])	Make synthetic data for the model and Gaussian noise provided.
residual(m, dobs[, f])	The data residual.

getAdc
getAdcDeriv
getInitialFieldsDeriv
getRHSDeriv

Galleries and Tutorials using SimPEG.electromagnetics.time_domain.Simulation3DElectricField

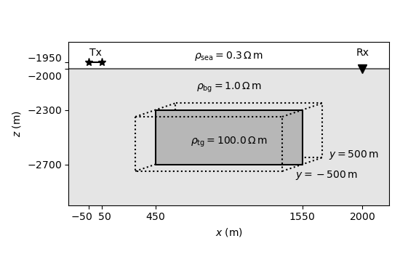
Time-domain CSEM for a resistive cube in a deep marine setting

Time-domain CSEM for a resistive cube in a deep marine setting

EM: TDEM: 1D: Inversion

EM: TDEM: 1D: Inversion

Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions

Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions