SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity#
- class SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity(mesh, survey=None, dt_threshold=1e-08, **kwargs)[source]#
Bases:
BaseTDEMSimulationStarting from the quasi-static E-B formulation of Maxwell’s equations (semi-discretized)
\[\begin{split}\mathbf{C} \mathbf{e} + \frac{\partial \mathbf{b}}{\partial t} = \mathbf{s_m} \\ \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e} \mathbf{e} = \mathbf{s_e}\end{split}\]where \(\mathbf{s_e}\) is an integrated quantity, we eliminate \(\mathbf{e}\) using
\[\mathbf{e} = \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}\]to obtain a second order semi-discretized system in \(\mathbf{b}\)
\[\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} + \frac{\partial \mathbf{b}}{\partial t} = \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e} + \mathbf{s_m}\]and moving everything except the time derivative to the rhs gives
\[\frac{\partial \mathbf{b}}{\partial t} = -\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} + \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e} + \mathbf{s_m}\]For the time discretization, we use backward euler. To solve for the \(n+1\) th time step, we have
\[\frac{\mathbf{b}^{n+1} - \mathbf{b}^{n}}{\mathbf{dt}} = -\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b}^{n+1} + \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}^{n+1} + \mathbf{s_m}^{n+1}\]re-arranging to put \(\mathbf{b}^{n+1}\) on the left hand side gives
\[(\mathbf{I} + \mathbf{dt} \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f}) \mathbf{b}^{n+1} = \mathbf{b}^{n} + \mathbf{dt}(\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}^{n+1} + \mathbf{s_m}^{n+1})\]Attributes
Cell center inner product matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Edge inner product matrix.
Edge inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Face inner product matrix.
Face inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Node inner product matrix.
Node inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
A list of solver objects to clean when the model is updated
SimPEG
Counterobject to store iterations and run-times.matrices to be deleted if the model for conductivity/resistivity is updated
The threshold used to determine if a previous matrix factor can be reused.
Mesh for the simulation.
The inversion model.
Magnetic permeability (h/m) physical property model.
Derivative of Magnetic Permeability (H/m) wrt the model.
Mapping of the inversion model to Magnetic Permeability (H/m).
Inverse magnetic permeability (m/h) physical property model.
Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
Mapping of the inversion model to Inverse Magnetic Permeability (m/H).
Total number of time steps.
True if a model is necessary
Electrical resistivity (ohm m) physical property model.
Derivative of Electrical resistivity (Ohm m) wrt the model.
Mapping of the inversion model to Electrical resistivity (Ohm m).
Path to directory where sensitivity file is stored.
Electrical conductivity (s/m) physical property model.
Derivative of Electrical conductivity (S/m) wrt the model.
Mapping of the inversion model to Electrical conductivity (S/m).
Numerical solver used in the forward simulation.
Solver-specific parameters.
Whether to store inner product matrices
The survey for the simulation Returns ------- SimPEG.electromagnetics.time_domain.survey.Survey
Initial time, in seconds, for the time-dependent forward simulation.
Time mesh for easy interpolation to observation times.
Time step lengths, in seconds, for the time domain simulation.
Evaluation times.
Verbose progress printout.
Adcinv
MccI
Vol
Methods
Fields_Derivsalias of
FieldsDerivativesEBJtvec(m, v[, f])Jvec computes the adjoint of the sensitivity times a vector
Jtvec_approx(m, v[, f])Approximation of the Jacobian transpose times a vector for the model provided.
Jvec(m, v[, f])Jvec computes the sensitivity times a vector
Jvec_approx(m, v[, f])Approximation of the Jacobian times a vector for the model provided.
MccMuDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccMuIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccMuiDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccMuiIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccRhoDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccRhoIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccSigmaDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccSigmaIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MeMuDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeMuIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeMuiDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeMuiIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeRhoDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeRhoIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeSigmaDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeSigmaIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MfMuDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfMuIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfMuiDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfMuiIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfRhoDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfRhoIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfSigmaDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfSigmaIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MnMuDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnMuIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnMuiDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnMuiIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnRhoDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnRhoIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnSigmaDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnSigmaIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
dpred([m, f])Predicted data for the model provided.
fields(m)Solve the forward problem for the fields.
fieldsPairalias of
Fields3DMagneticFluxDensitygetAdiag(tInd)System matrix at a given time index
getAdiagDeriv(tInd, u, v[, adjoint])Derivative of ADiag
getAsubdiag(tInd)Matrix below the diagonal
Ask the sources for initial fields
getRHS(tInd)Assemble the RHS
getRHSDeriv(tInd, src, v[, adjoint])Derivative of the RHS
getSourceTerm(tInd)Assemble the source term.
make_synthetic_data(m[, relative_error, ...])Make synthetic data for the model and Gaussian noise provided.
residual(m, dobs[, f])The data residual.
getAsubdiagDeriv
getInitialFieldsDeriv
Galleries and Tutorials using SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity#
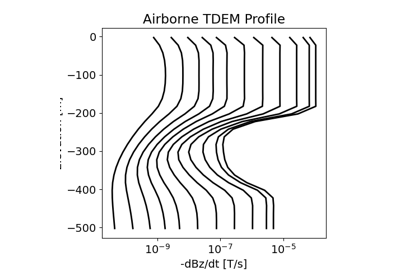
3D Forward Simulation for Transient Response on a Cylindrical Mesh