SimPEG.maps.ParametricCircleMap#
- class SimPEG.maps.ParametricCircleMap(mesh, logSigma=True, slope=0.1)[source]#
Bases:
IdentityMapMapping for a parameterized circle.
Define the mapping from a parameterized model for a circle in a wholespace to all cells within a 2D mesh. For a circle within a wholespace, the model is defined by 5 parameters: the background physical property value (\(\sigma_0\)), the physical property value for the circle (\(\sigma_c\)), the x location \(x_0\) and y location \(y_0\) for center of the circle, and the circle’s radius (\(R\)).
Let \(\mathbf{m} = [\sigma_0, \sigma_1, x_0, y_0, R]\) be the set of model parameters the defines a circle within a wholespace. The mapping \(\mathbf{u}(\mathbf{m})\) from the parameterized model to all cells within a 2D mesh is given by:
\[\mathbf{u}(\mathbf{m}) = \sigma_0 + (\sigma_1 - \sigma_0) \bigg [ \frac{1}{2} + \pi^{-1} \arctan \bigg ( a \big [ \sqrt{(\mathbf{x_c}-x_0)^2 + (\mathbf{y_c}-y_0)^2} - R \big ] \bigg ) \bigg ]\]where \(\mathbf{x_c}\) and \(\mathbf{y_c}\) are vectors storing the x and y positions of all cell centers for the 2D mesh and \(a\) is a user-defined constant which defines the sharpness of boundary of the circular structure.
- Parameters:
- mesh
discretize.BaseMesh A 2D discretize mesh
- logSigmabool
If
True, parameters \(\sigma_0\) and \(\sigma_1\) represent the natural log of the physical property values for the background and circle, respectively.- slope
float A constant for defining the sharpness of the boundary between the circle and the wholespace. The sharpness increases as slope is increased.
- mesh
Examples
Here we define the parameterized model for a circle in a wholespace. We then create and use a
ParametricCircleMapto map the model to a 2D mesh.>>> from SimPEG.maps import ParametricCircleMap >>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt
>>> h = 0.5*np.ones(20) >>> mesh = TensorMesh([h, h])
>>> sigma0, sigma1, x0, y0, R = 0., 10., 4., 6., 2. >>> model = np.r_[sigma0, sigma1, x0, y0, R] >>> mapping = ParametricCircleMap(mesh, logSigma=False, slope=2)
>>> fig = plt.figure(figsize=(5, 5)) >>> ax = fig.add_subplot(111) >>> mesh.plot_image(mapping * model, ax=ax)
(
Source code,png,pdf)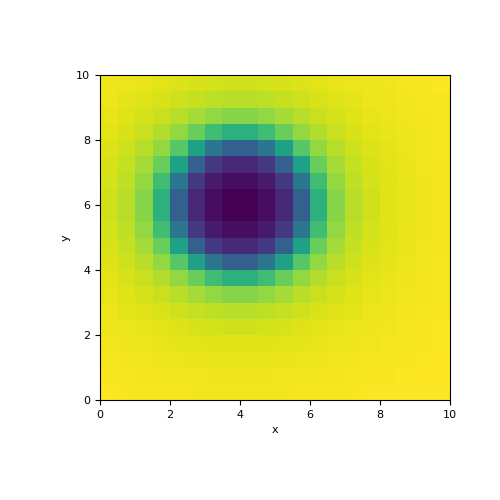
Attributes
Determine whether or not this mapping is a linear operation.
Whether the input needs to be transformed by an exponential
The mesh used for the mapping
Number of parameters the mapping acts on; i.e. 5.
Dimensions of the mapping operator
Sharpness of the boundary.
Methods
deriv(m[, v])Derivative of the mapping with respect to the input parameters.
dot(map1)Multiply two mappings to create a
SimPEG.maps.ComboMap.inverse(D)The transform inverse is not implemented.
test([m, num])Derivative test for the mapping.