SimPEG.maps.ParametricEllipsoid#
- class SimPEG.maps.ParametricEllipsoid(mesh, **kwargs)[source]#
Bases:
ParametricBlockMapping for a rectangular block within a wholespace.
This mapping is used when the cells lying below the Earth’s surface can be parameterized by an ellipsoid within a homogeneous medium. The model is defined by the physical property value for the background (\(\sigma_0\)), the physical property value for the layer (\(\sigma_b\)), parameters for the center of the ellipsoid (\(x_b [,y_b, z_b]\)) and parameters for the dimensions along each Cartesian direction (\(dx [,dy, dz]\))
For this mapping, the set of input model parameters are organized:
\[\begin{split}\mathbf{m} = \begin{cases} 1D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx] \\ 2D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx,\; y_b , \; dy] \\ 3D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx,\; y_b , \; dy,\; z_b , \; dz] \end{cases}\end{split}\]The mapping \(\mathbf{u}(\mathbf{m})\) from the model to the mesh is given by:
\[\mathbf{u}(\mathbf{m}) = \sigma_0 + (\sigma_b - \sigma_0) \bigg [ \frac{1}{2} + \pi^{-1} \arctan \bigg ( a \, \boldsymbol{\eta} \big ( x_b, y_b, z_b, dx, dy, dz \big ) \bigg ) \bigg ]\]where a is a parameter that impacts the sharpness of the arctan function, and
\[\boldsymbol{\eta} \big ( x_b, y_b, z_b, dx, dy, dz \big ) = 1 - \sum_{\xi \in (x,y,z)} \bigg [ \bigg ( \frac{2(\boldsymbol{\xi_c} - \xi_b)}{d\xi} \bigg )^2 + \varepsilon^2 \bigg ]\]\(\boldsymbol{\xi_c}\) is a place holder for vectors containing the x, [y and z] cell center locations of the mesh, \(\xi_b\) is a placeholder for the x[, y and z] location for the center of the block, and \(d\xi\) is a placeholder for the x[, y and z] dimensions of the block.
- Parameters:
- mesh
discretize.BaseMesh A discretize mesh
- indActive
numpy.ndarray Active cells array. Can be a boolean
numpy.ndarrayof length mesh.nC or anumpy.ndarrayofintcontaining the indices of the active cells.- slope
float Directly define the constant a in the mapping function which defines the sharpness of the boundaries.
- slopeFact
float Scaling factor for the sharpness of the boundaries based on cell size. Using this option, we set a = slopeFact / dh.
- epsilon
float Epsilon value used in the ekblom representation of the block
- mesh
Examples
In this example, we define an ellipse in a wholespace whose interface is sharp. We construct the mapping from the model to the set of active cells (i.e. below the surface), We then use an active cells mapping to map from the set of active cells to all cells in the mesh.
>>> from SimPEG.maps import ParametricEllipsoid, InjectActiveCells >>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt
>>> dh = 0.5*np.ones(20) >>> mesh = TensorMesh([dh, dh]) >>> ind_active = mesh.cell_centers[:, 1] < 8
>>> sig0, sigb, xb, Lx, yb, Ly = 5., 10., 5., 4., 4., 3. >>> model = np.r_[sig0, sigb, xb, Lx, yb, Ly]
>>> ellipsoid_map = ParametricEllipsoid(mesh, indActive=ind_active) >>> act_map = InjectActiveCells(mesh, ind_active, 0.)
>>> fig = plt.figure(figsize=(5, 5)) >>> ax = fig.add_subplot(111) >>> mesh.plot_image(act_map * ellipsoid_map * model, ax=ax)
(
Source code,png,pdf)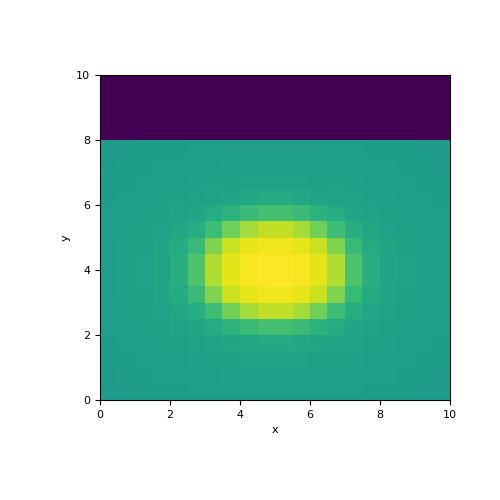
Attributes
epsilon value used in the ekblom representation of the block.
Determine whether or not this mapping is a linear operation.
The mesh used for the mapping
Number of parameters the mapping acts on.
p-value used in the ekblom representation of the block.
Dimensions of the mapping
Defines the sharpness of the boundaries.
Defines the slope scaled by the mesh.
X cell center locations (active) for the output of the mapping.
Y cell center locations (active) for the output of the mapping.
Z cell center locations (active) for the output of the mapping.
indActive
Methods
deriv(m)Derivative of the mapping with respect to the input parameters.
dot(map1)Multiply two mappings to create a
SimPEG.maps.ComboMap.inverse(D)The transform inverse is not implemented.
mDict(m)Return model parameters as a dictionary.
test([m, num])Derivative test for the mapping.