Magnetic inversion on a TreeMesh

In this example, we demonstrate the use of a Magnetic Vector Inverison on 3D TreeMesh for the inversion of magnetic data.

The inverse problem uses the :class:’simpeg.regularization.VectorAmplitude’ regularization borrowed from …

from simpeg import (
    data,
    data_misfit,
    directives,
    maps,
    inverse_problem,
    optimization,
    inversion,
    regularization,
)

from simpeg import utils
from simpeg.utils import mkvc, sdiag

from discretize.utils import mesh_builder_xyz, refine_tree_xyz, active_from_xyz
from simpeg.potential_fields import magnetics
import numpy as np
import matplotlib.pyplot as plt


# sphinx_gallery_thumbnail_number = 3

Setup

Define the survey and model parameters

First we need to define the direction of the inducing field As a simple case, we pick a vertical inducing field of magnitude 50,000 nT.

np.random.seed(1)
# We will assume a vertical inducing field
h0_amplitude, h0_inclination, h0_declination = (50000.0, 90.0, 0.0)

# Create grid of points for topography
# Lets create a simple Gaussian topo and set the active cells
[xx, yy] = np.meshgrid(np.linspace(-200, 200, 50), np.linspace(-200, 200, 50))
b = 100
A = 50
zz = A * np.exp(-0.5 * ((xx / b) ** 2.0 + (yy / b) ** 2.0))
topo = np.c_[utils.mkvc(xx), utils.mkvc(yy), utils.mkvc(zz)]

# Create an array of observation points
xr = np.linspace(-100.0, 100.0, 20)
yr = np.linspace(-100.0, 100.0, 20)
X, Y = np.meshgrid(xr, yr)
Z = A * np.exp(-0.5 * ((X / b) ** 2.0 + (Y / b) ** 2.0)) + 5

# Create a MAGsurvey
xyzLoc = np.c_[mkvc(X.T), mkvc(Y.T), mkvc(Z.T)]
rxLoc = magnetics.receivers.Point(xyzLoc)
srcField = magnetics.sources.UniformBackgroundField(
    receiver_list=[rxLoc],
    amplitude=h0_amplitude,
    inclination=h0_inclination,
    declination=h0_declination,
)
survey = magnetics.survey.Survey(srcField)

Inversion Mesh

Here, we create a TreeMesh with base cell size of 5 m.

# Create a mesh
h = [5, 5, 5]
padDist = np.ones((3, 2)) * 100

mesh = mesh_builder_xyz(
    xyzLoc, h, padding_distance=padDist, depth_core=100, mesh_type="tree"
)
mesh = refine_tree_xyz(
    mesh, topo, method="surface", octree_levels=[2, 6], finalize=True
)


# Define an active cells from topo
actv = active_from_xyz(mesh, topo)
nC = int(actv.sum())

/home/vsts/work/1/s/examples/03-magnetics/plot_inv_mag_MVI_VectorAmplitude.py:88: DeprecationWarning:

The surface option is deprecated as of `0.9.0` please update your code to use the `TreeMesh.refine_surface` functionality. It will be removed in a future version of discretize.

Forward modeling data

We can now create a magnetization model and generate data.

model_azm_dip = np.zeros((mesh.nC, 2))
model_amp = np.ones(mesh.nC) * 1e-8
ind = utils.model_builder.get_indices_block(
    np.r_[-30, -20, -10],
    np.r_[30, 20, 25],
    mesh.gridCC,
)[0]
model_amp[ind] = 0.05
model_azm_dip[ind, 0] = 45.0
model_azm_dip[ind, 1] = 90.0

# Remove air cells
model_azm_dip = model_azm_dip[actv, :]
model_amp = model_amp[actv]
model = sdiag(model_amp) * utils.mat_utils.dip_azimuth2cartesian(
    model_azm_dip[:, 0], model_azm_dip[:, 1]
)

# Create reduced identity map
idenMap = maps.IdentityMap(nP=nC * 3)

# Create the simulation
simulation = magnetics.simulation.Simulation3DIntegral(
    survey=survey, mesh=mesh, chiMap=idenMap, ind_active=actv, model_type="vector"
)

# Compute some data and add some random noise
d = simulation.dpred(mkvc(model))
std = 10  # nT
synthetic_data = d + np.random.randn(len(d)) * std
wd = np.ones(len(d)) * std

# Assign data and uncertainties to the survey
data_object = data.Data(survey, dobs=synthetic_data, standard_deviation=wd)

# Create a projection matrix for plotting later
actv_plot = maps.InjectActiveCells(mesh, actv, np.nan)

Inversion

We can now attempt the inverse calculations.

# Create sensitivity weights from our linear forward operator
rxLoc = survey.source_field.receiver_list[0].locations

# This Mapping connects the regularizations for the three-component
# vector model
wires = maps.Wires(("p", nC), ("s", nC), ("t", nC))
m0 = np.ones(3 * nC) * 1e-4  # Starting model

# Create the regularization on the amplitude of magnetization
reg = regularization.VectorAmplitude(
    mesh,
    mapping=idenMap,
    active_cells=actv,
    reference_model_in_smooth=True,
    norms=[0.0, 2.0, 2.0, 2.0],
    gradient_type="total",
)

# Data misfit function
dmis = data_misfit.L2DataMisfit(simulation=simulation, data=data_object)
dmis.W = 1.0 / data_object.standard_deviation

# The optimization scheme
opt = optimization.ProjectedGNCG(
    maxIter=20, lower=-10, upper=10.0, maxIterLS=20, maxIterCG=20, tolCG=1e-4
)

# The inverse problem
invProb = inverse_problem.BaseInvProblem(dmis, reg, opt)

# Estimate the initial beta factor
betaest = directives.BetaEstimate_ByEig(beta0_ratio=1e1)

# Add sensitivity weights
sensitivity_weights = directives.UpdateSensitivityWeights()

# Here is where the norms are applied
IRLS = directives.Update_IRLS(f_min_change=1e-3, max_irls_iterations=10, beta_tol=5e-1)

# Pre-conditioner
update_Jacobi = directives.UpdatePreconditioner()


inv = inversion.BaseInversion(
    invProb, directiveList=[sensitivity_weights, IRLS, update_Jacobi, betaest]
)

# Run the inversion
mrec = inv.run(m0)

Running inversion with SimPEG v0.22.0
simpeg.InvProblem will set Regularization.reference_model to m0.
simpeg.InvProblem will set Regularization.reference_model to m0.
simpeg.InvProblem will set Regularization.reference_model to m0.
simpeg.InvProblem will set Regularization.reference_model to m0.

                    simpeg.InvProblem is setting bfgsH0 to the inverse of the eval2Deriv.
                    ***Done using the default solver Pardiso and no solver_opts.***

model has any nan: 0
=============================== Projected GNCG ===============================
  #     beta     phi_d     phi_m       f      |proj(x-g)-x|  LS    Comment
-----------------------------------------------------------------------------
x0 has any nan: 0
   0  1.32e+05  1.19e+04  0.00e+00  1.19e+04    2.43e+03      0
   1  6.58e+04  6.96e+03  1.54e-02  7.97e+03    2.02e+03      0
   2  3.29e+04  4.72e+03  3.90e-02  6.01e+03    1.86e+03      0   Skip BFGS
   3  1.65e+04  2.75e+03  8.17e-02  4.09e+03    1.74e+03      0   Skip BFGS
   4  8.23e+03  1.36e+03  1.41e-01  2.52e+03    1.61e+03      0   Skip BFGS
   5  4.11e+03  6.06e+02  2.04e-01  1.45e+03    1.48e+03      0   Skip BFGS
Reached starting chifact with l2-norm regularization: Start IRLS steps...
irls_threshold 0.008916586712511429
   6  2.06e+03  2.62e+02  4.65e-01  1.22e+03    1.00e+03      0   Skip BFGS
   7  2.06e+03  2.05e+02  7.17e-01  1.68e+03    1.46e+03      0
   8  2.06e+03  3.28e+02  9.28e-01  2.24e+03    1.58e+03      0
   9  2.06e+03  5.02e+02  1.14e+00  2.86e+03    1.71e+03      0
  10  1.34e+03  7.18e+02  1.16e+00  2.28e+03    1.44e+03      0
  11  9.50e+02  6.03e+02  1.24e+00  1.78e+03    1.37e+03      0   Skip BFGS
  12  9.50e+02  5.27e+02  1.22e+00  1.68e+03    1.55e+03      0   Skip BFGS
  13  9.50e+02  5.54e+02  1.09e+00  1.59e+03    1.43e+03      0
  14  9.50e+02  5.56e+02  1.01e+00  1.51e+03    1.38e+03      0   Skip BFGS
  15  9.50e+02  5.52e+02  9.43e-01  1.45e+03    1.34e+03      0   Skip BFGS
Reach maximum number of IRLS cycles: 10
------------------------- STOP! -------------------------
1 : |fc-fOld| = 0.0000e+00 <= tolF*(1+|f0|) = 1.1929e+03
1 : |xc-x_last| = 2.7268e-02 <= tolX*(1+|x0|) = 1.0290e-01
0 : |proj(x-g)-x|    = 1.3377e+03 <= tolG          = 1.0000e-01
0 : |proj(x-g)-x|    = 1.3377e+03 <= 1e3*eps       = 1.0000e-02
0 : maxIter   =      20    <= iter          =     16
------------------------- DONE! -------------------------

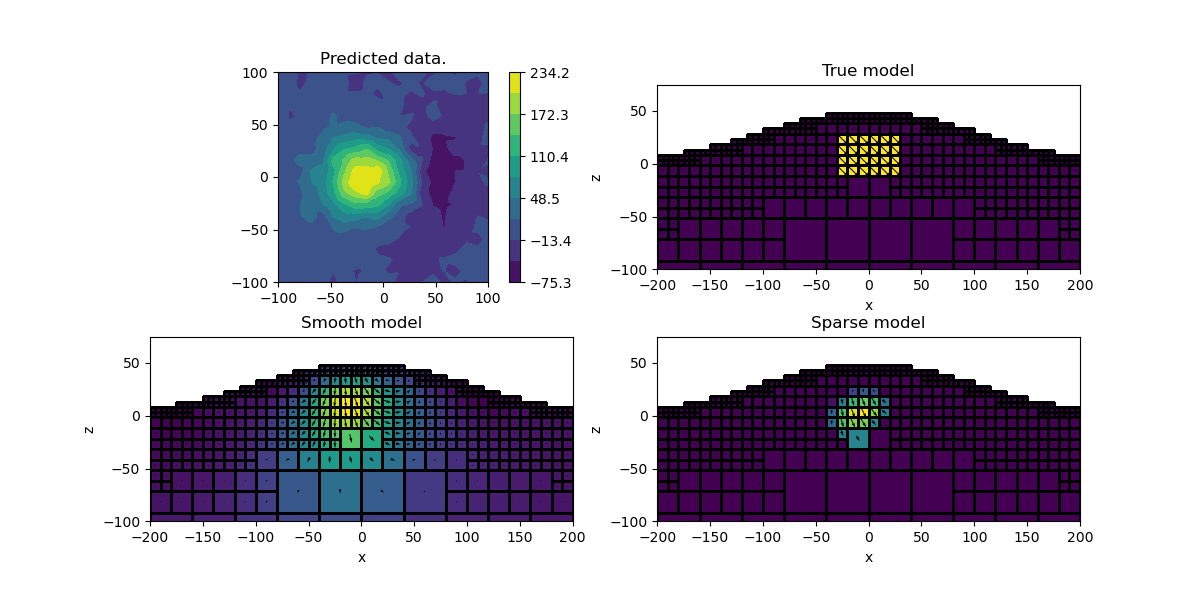
Final Plot

Let’s compare the smooth and compact model

plt.figure(figsize=(12, 6))
ax = plt.subplot(2, 2, 1)
im = utils.plot_utils.plot2Ddata(xyzLoc, synthetic_data, ax=ax)
plt.colorbar(im[0])
ax.set_title("Predicted data.")
plt.gca().set_aspect("equal", adjustable="box")

for ii, (title, mvec) in enumerate(
    [("True model", model), ("Smooth model", invProb.l2model), ("Sparse model", mrec)]
):
    ax = plt.subplot(2, 2, ii + 2)
    mesh.plot_slice(
        actv_plot * mvec.reshape((-1, 3), order="F"),
        v_type="CCv",
        view="vec",
        ax=ax,
        normal="Y",
        grid=True,
        quiver_opts={
            "pivot": "mid",
            "scale": 8 * np.abs(mvec).max(),
            "scale_units": "inches",
        },
    )
    ax.set_xlim([-200, 200])
    ax.set_ylim([-100, 75])
    ax.set_title(title)
    ax.set_xlabel("x")
    ax.set_ylabel("z")
    plt.gca().set_aspect("equal", adjustable="box")

plt.show()

print("END")
# Plot the final predicted data and the residual
# plt.figure()
# ax = plt.subplot(1, 2, 1)
# utils.plot_utils.plot2Ddata(xyzLoc, invProb.dpred, ax=ax)
# ax.set_title("Predicted data.")
# plt.gca().set_aspect("equal", adjustable="box")
#
# ax = plt.subplot(1, 2, 2)
# utils.plot_utils.plot2Ddata(xyzLoc, synthetic_data - invProb.dpred, ax=ax)
# ax.set_title("Data residual.")
# plt.gca().set_aspect("equal", adjustable="box")

END

Estimated memory usage: 137 MB