simpeg.data_misfit.BaseDataMisfit#
- class simpeg.data_misfit.BaseDataMisfit(data, simulation, debug=False, counter=None, **kwargs)[source]#
Bases:
L2ObjectiveFunctionBase data misfit class.
Inherit this class to build your own data misfit function. The
BaseDataMisfitclass inherits thesimpeg.objective_function.L2ObjectiveFunction. And as a result, it is limited to building data misfit functions of the form:Important
This class is not meant to be instantiated. You should inherit from it to create your own data misfit class.
\[\phi_d (\mathbf{m}) = \| \mathbf{W} f(\mathbf{m}) \|_2^2\]where \(\mathbf{m}\) is the model vector, \(\mathbf{W}\) is a linear weighting matrix, and \(f\) is a mapping function that acts on the model.
- Parameters:
- data
simpeg.data.Data A SimPEG data object.
- simulation
simpeg.simulation.BaseSimulation A SimPEG simulation object.
- debugbool
Print debugging information.
- counter
Noneorsimpeg.utils.Counter Assign a SimPEG
Counterobject to store iterations and run-times.
- data
Attributes
The data weighting matrix.
SimPEG
Counterobject to store iterations and run-times.A SimPEG data object.
Print debugging information.
Mapping from the model to the quantity evaluated in the object function.
Number of data.
Number of model parameters.
Shape of the Jacobian.
A SimPEG simulation object.
Methods
__call__(m)Evaluate the objective function for a given model.
deriv(m)Gradient of the objective function evaluated for the model provided.
deriv2(m[, v])Hessian of the objective function evaluated for the model provided.
map_classalias of
IdentityMapresidual(m[, f])Computes the data residual vector for a given model.
test([x, num, random_seed])Run a convergence test on both the first and second derivatives.
Galleries and Tutorials using simpeg.data_misfit.BaseDataMisfit#
Method of Equivalent Sources for Removing VRM Responses
Petrophysically guided inversion (PGI): Linear example
Petrophysically guided inversion: Joint linear example with nonlinear relationships
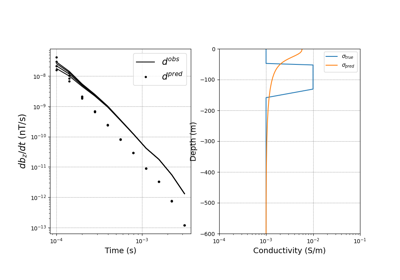
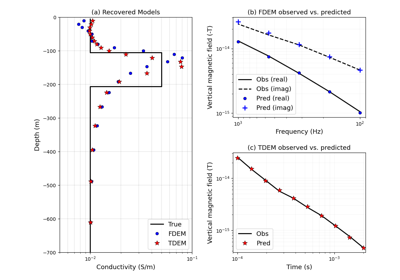
Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
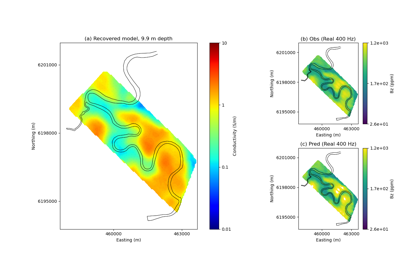
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion
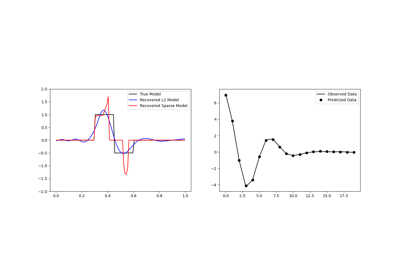
Sparse Inversion with Iteratively Re-Weighted Least-Squares
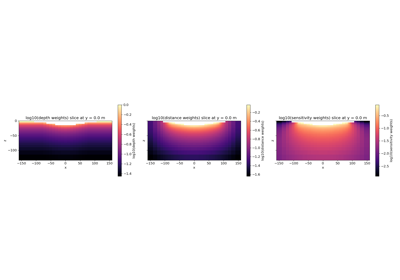
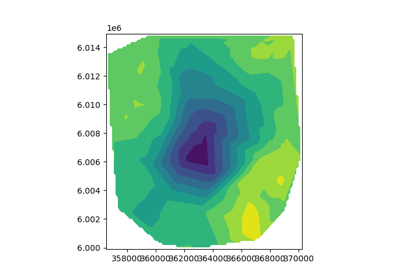
Compare weighting strategy with Inversion of surface Gravity Anomaly Data
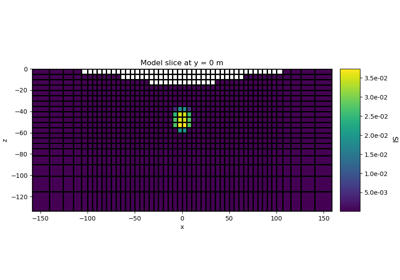
Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh
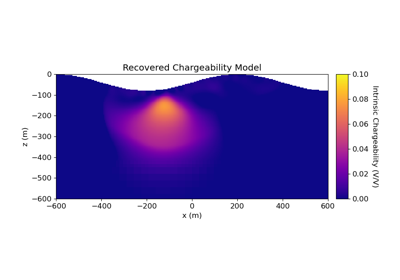
2.5D DC Resistivity and IP Least-Squares Inversion
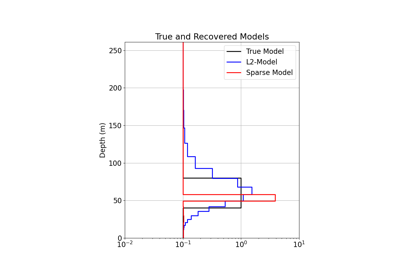
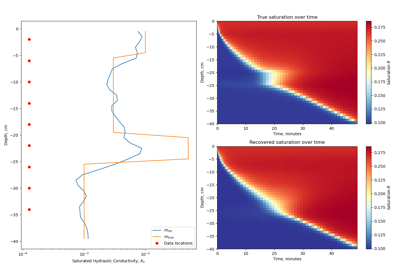
1D Inversion of Time-Domain Data for a Single Sounding
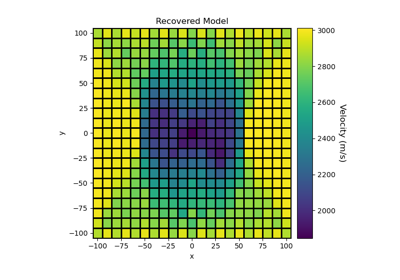
Sparse Norm Inversion of 2D Seismic Tomography Data
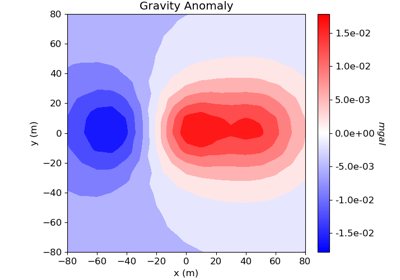
Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data

Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information