simpeg.maps.IdentityMap#
- class simpeg.maps.IdentityMap(mesh=None, nP=None, **kwargs)[source]#
Bases:
objectIdentity mapping and the base mapping class for all other SimPEG mappings.
The
IdentityMapclass is used to define the mapping when the model parameters are the same as the parameters used in the forward simulation. For a discrete set of model parameters \(\mathbf{m}\), the mapping \(\mathbf{u}(\mathbf{m})\) is equivalent to applying the identity matrix; i.e.:\[\mathbf{u}(\mathbf{m}) = \mathbf{Im}\]The
IdentityMapalso acts as the base class for all other SimPEG mapping classes.Using the mesh or nP input arguments, the dimensions of the corresponding mapping operator can be permanently set; i.e. (mesh.nC, mesh.nC) or (nP, nP). However if both input arguments mesh and nP are
None, the shape of mapping operator is arbitrary and can act on any vector; i.e. has shape (*,*).- Parameters:
- mesh
discretize.BaseMesh The number of parameters accepted by the mapping is set to equal the number of mesh cells.
- nP
int,or‘*’ Set the number of parameters accepted by the mapping directly. Used if the number of parameters is known. Used generally when the number of parameters is not equal to the number of cells in a mesh.
- mesh
Attributes
Determine whether or not this mapping is a linear operation.
The mesh used for the mapping
Number of parameters the mapping acts on.
Dimensions of the mapping operator
Methods
deriv(m[, v])Derivative of the mapping with respect to the input parameters.
dot(map1)Multiply two mappings to create a
simpeg.maps.ComboMap.inverse(D)The transform inverse is not implemented.
test([m, num, random_seed])Derivative test for the mapping.
Galleries and Tutorials using simpeg.maps.IdentityMap#

Time-domain CSEM for a resistive cube in a deep marine setting
Predict Response from a Conductive and Magnetically Viscous Earth
Method of Equivalent Sources for Removing VRM Responses
Petrophysically guided inversion (PGI): Linear example
Petrophysically guided inversion: Joint linear example with nonlinear relationships
Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion

Sparse Inversion with Iteratively Re-Weighted Least-Squares
Forward Simulation of Gravity Anomaly Data on a Tensor Mesh
Forward Simulation of Gradiometry Data on a Tree Mesh
Compare weighting strategy with Inversion of surface Gravity Anomaly Data
Forward Simulation of Total Magnetic Intensity Data
Forward Simulation of Gradiometry Data for Magnetic Vector Models

Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh
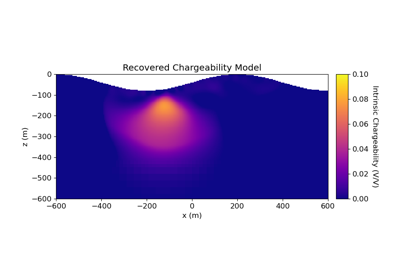
2.5D DC Resistivity and IP Least-Squares Inversion
1D Forward Simulation for a Susceptible and Chargeable Earth

1D Forward Simulation with Chargeable and/or Magnetic Viscosity
3D Forward Simulation for Transient Response on a Cylindrical Mesh
1D Inversion of Time-Domain Data for a Single Sounding

Forward Simulation for Straight Ray Tomography in 2D
Sparse Norm Inversion of 2D Seismic Tomography Data

Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data

Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information