SimPEG.maps.ParametricEllipsoid

class SimPEG.maps.ParametricEllipsoid(mesh, **kwargs)

Bases: ParametricBlock

Mapping for a rectangular block within a wholespace.

This mapping is used when the cells lying below the Earth’s surface can be parameterized by an ellipsoid within a homogeneous medium. The model is defined by the physical property value for the background (\(\sigma_0\)), the physical property value for the layer (\(\sigma_b\)), parameters for the center of the ellipsoid (\(x_b [,y_b, z_b]\)) and parameters for the dimensions along each Cartesian direction (\(dx [,dy, dz]\))

For this mapping, the set of input model parameters are organized:

\[\begin{split}\mathbf{m} = \begin{cases} 1D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx] \\ 2D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx,\; y_b , \; dy] \\ 3D: \;\; [\sigma_0, \;\sigma_b,\; x_b , \; dx,\; y_b , \; dy,\; z_b , \; dz] \end{cases}\end{split}\]

The mapping \(\mathbf{u}(\mathbf{m})\) from the model to the mesh is given by:

\[\mathbf{u}(\mathbf{m}) = \sigma_0 + (\sigma_b - \sigma_0) \bigg [ \frac{1}{2} + \pi^{-1} \arctan \bigg ( a \, \boldsymbol{\eta} \big ( x_b, y_b, z_b, dx, dy, dz \big ) \bigg ) \bigg ]\]

where a is a parameter that impacts the sharpness of the arctan function, and

\[\boldsymbol{\eta} \big ( x_b, y_b, z_b, dx, dy, dz \big ) = 1 - \sum_{\xi \in (x,y,z)} \bigg [ \bigg ( \frac{2(\boldsymbol{\xi_c} - \xi_b)}{d\xi} \bigg )^2 + \varepsilon^2 \bigg ]\]

\(\boldsymbol{\xi_c}\) is a place holder for vectors containing the x, [y and z] cell center locations of the mesh, \(\xi_b\) is a placeholder for the x[, y and z] location for the center of the block, and \(d\xi\) is a placeholder for the x[, y and z] dimensions of the block.

Parameters:

meshdiscretize.BaseMesh

A discretize mesh

indActivenumpy.ndarray

Active cells array. Can be a boolean numpy.ndarray of length mesh.nC or a numpy.ndarray of int containing the indices of the active cells.

slopefloat

Directly define the constant a in the mapping function which defines the sharpness of the boundaries.

slopeFactfloat

Scaling factor for the sharpness of the boundaries based on cell size. Using this option, we set a = slopeFact / dh.

epsilonfloat

Epsilon value used in the ekblom representation of the block

Examples

In this example, we define an ellipse in a wholespace whose interface is sharp. We construct the mapping from the model to the set of active cells (i.e. below the surface), We then use an active cells mapping to map from the set of active cells to all cells in the mesh.

>>> from SimPEG.maps import ParametricEllipsoid, InjectActiveCells
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt

>>> dh = 0.5*np.ones(20)
>>> mesh = TensorMesh([dh, dh])
>>> ind_active = mesh.cell_centers[:, 1] < 8

>>> sig0, sigb, xb, Lx, yb, Ly = 5., 10., 5., 4., 4., 3.
>>> model = np.r_[sig0, sigb, xb, Lx, yb, Ly]

>>> ellipsoid_map = ParametricEllipsoid(mesh, indActive=ind_active)
>>> act_map = InjectActiveCells(mesh, ind_active, 0.)

>>> fig = plt.figure(figsize=(5, 5))
>>> ax = fig.add_subplot(111)
>>> mesh.plot_image(act_map * ellipsoid_map * model, ax=ax)

(Source code, png, pdf)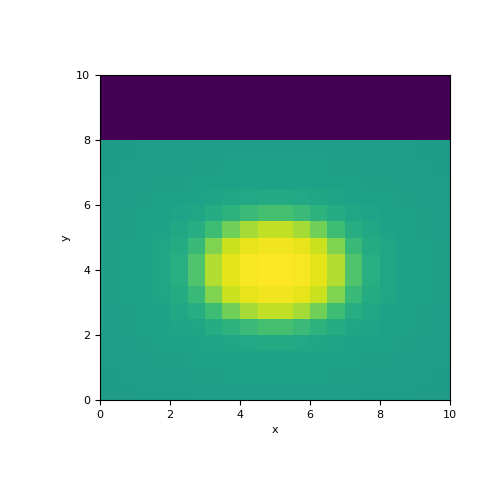

Attributes

epsilon	epsilon value used in the ekblom representation of the block.
is_linear	Determine whether or not this mapping is a linear operation.
mesh	The mesh used for the mapping
nP	Number of parameters the mapping acts on.
p	p-value used in the ekblom representation of the block.
shape	Dimensions of the mapping
slope	Defines the sharpness of the boundaries.
slopeFact	Defines the slope scaled by the mesh.
x	X cell center locations (active) for the output of the mapping.
y	Y cell center locations (active) for the output of the mapping.
z	Z cell center locations (active) for the output of the mapping.

indActive

Methods

deriv(m)	Derivative of the mapping with respect to the input parameters.
dot(map1)	Multiply two mappings to create a SimPEG.maps.ComboMap.
inverse(D)	The transform inverse is not implemented.
mDict(m)	Return model parameters as a dictionary.
test([m, num])	Derivative test for the mapping.