SimPEG.objective_function.L2ObjectiveFunction#
- class SimPEG.objective_function.L2ObjectiveFunction(nP=None, mapping=None, W=None, has_fields=False, counter=None, debug=False)[source]#
Bases:
BaseObjectiveFunctionWeighted least-squares objective function class.
Weighting least-squares objective functions in SimPEG are defined as follows:
\[\phi = \big \| \mathbf{W} f(\mathbf{m}) \big \|_2^2\]where \(\mathbf{m}\) are the model parameters, \(f\) is a mapping operator, and \(\mathbf{W}\) is the weighting matrix.
- Parameters:
- nP
int Number of model parameters.
- mapping
SimPEG.mapping.BaseMap A SimPEG mapping object that maps from the model space to the quantity evaluated in the objective function.
- W
Noneorscipy.sparse.csr_matrix The weighting matrix applied in the objective function. By default, this is set to the identity matrix.
- has_fieldsbool
If
True, predicted fields for a simulation and a given model can be used to evaluate the objective function quickly.- counter
NoneorSimPEG.utils.Counter Assign a SimPEG
Counterobject to store iterations and run-times.- debugbool
Print debugging information.
- nP
Attributes
Weighting matrix applied in the objective function.
Mapping from the model to the quantity evaluated in the object function.
Number of model parameters.
Methods
__call__(m)Evaluate the objective function for a given model.
deriv(m)Gradient of the objective function evaluated for the model provided.
deriv2(m[, v])Hessian of the objective function evaluated for the model provided.
map_classalias of
IdentityMaptest([x, num])Run a convergence test on both the first and second derivatives.
Galleries and Tutorials using SimPEG.objective_function.L2ObjectiveFunction#
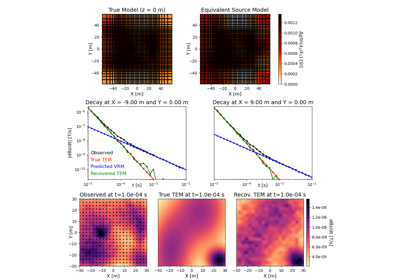
Method of Equivalent Sources for Removing VRM Responses

Petrophysically guided inversion (PGI): Linear example
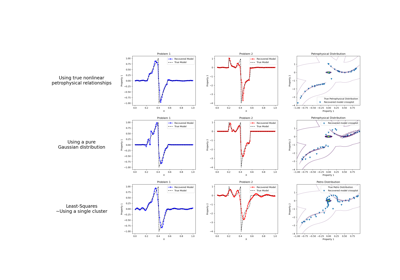
Petrophysically guided inversion: Joint linear example with nonlinear relationships

Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
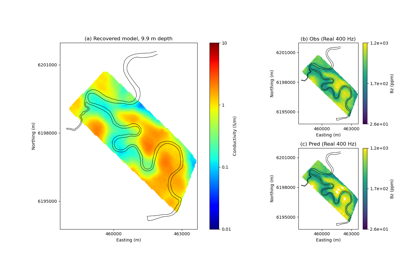
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion
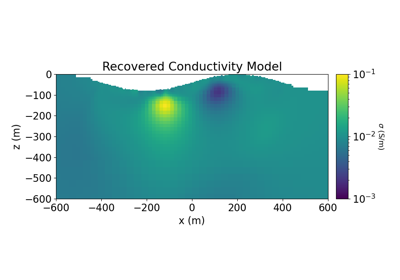
Sparse Inversion with Iteratively Re-Weighted Least-Squares

Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information

Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data
2.5D DC Resistivity and IP Least-Squares Inversion
Sparse Norm Inversion of 2D Seismic Tomography Data
1D Inversion of Time-Domain Data for a Single Sounding
Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh