SimPEG.simulation.BaseSimulation#
- class SimPEG.simulation.BaseSimulation(mesh=None, survey=None, solver=None, solver_opts=None, sensitivity_path=None, counter=None, verbose=False, **kwargs)[source]#
Bases:
HasModelBase class for all geophysical forward simulations in SimPEG.
The
BaseSimulationclass defines properties and methods inherited by practical simulation classes in SimPEG.Important
This class is not meant to be instantiated. You should inherit from it to create your own simulation class.
- Parameters:
- mesh
discretize.base.BaseMesh,optional Mesh on which the forward problem is discretized.
- survey
SimPEG.survey.BaseSurvey,optional The survey for the simulation.
- solver
Noneorpymatsolver.base.Base,optional Numerical solver used to solve the forward problem. If
None, an appropriate solver specific to the simulation class is set by default.- solver_opts
dict,optional Solver-specific parameters. If
None, default parameters are used for the solver set bysolver. Otherwise, thedictmust contain appropriate pairs of keyword arguments and parameter values for the solver. Please visit pymatsolver to learn more about solvers and their parameters.- sensitivity_path
str,optional Path to directory where sensitivity file is stored.
- counter
NoneorSimPEG.utils.Counter SimPEG
Counterobject to store iterations and run-times.- verbosebool,
optional Verbose progress printout.
- mesh
Attributes
A list of solver objects to clean when the model is updated
SimPEG
Counterobject to store iterations and run-times.A list of properties stored on this object to delete when the model is updated
Mesh for the simulation.
The inversion model.
True if a model is necessary
Path to directory where sensitivity file is stored.
Numerical solver used in the forward simulation.
Solver-specific parameters.
The survey for the simulation.
Verbose progress printout.
Methods
Jtvec(m, v[, f])Compute the Jacobian transpose times a vector for the model provided.
Jtvec_approx(m, v[, f])Approximation of the Jacobian transpose times a vector for the model provided.
Jvec(m, v[, f])Compute the Jacobian times a vector for the model provided.
Jvec_approx(m, v[, f])Approximation of the Jacobian times a vector for the model provided.
dpred([m, f])Predicted data for the model provided.
fields([m])Return the computed geophysical fields for the model provided.
make_synthetic_data(m[, relative_error, ...])Make synthetic data for the model and Gaussian noise provided.
residual(m, dobs[, f])The data residual.
Galleries and Tutorials using SimPEG.simulation.BaseSimulation#
Time-domain CSEM for a resistive cube in a deep marine setting
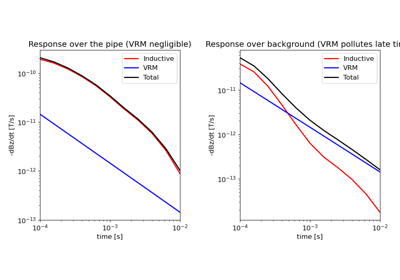
Predict Response from a Conductive and Magnetically Viscous Earth
Method of Equivalent Sources for Removing VRM Responses

Petrophysically guided inversion (PGI): Linear example
Petrophysically guided inversion: Joint linear example with nonlinear relationships

Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion
Sparse Inversion with Iteratively Re-Weighted Least-Squares
1D Forward Simulation for a Susceptible and Chargeable Earth

Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information

Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data
2.5D DC Resistivity and IP Least-Squares Inversion
Forward Simulation for Straight Ray Tomography in 2D
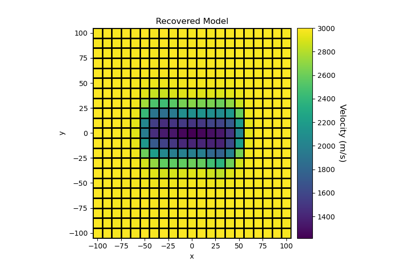
Sparse Norm Inversion of 2D Seismic Tomography Data
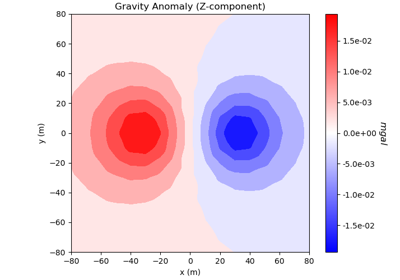
Forward Simulation of Gravity Anomaly Data on a Tensor Mesh
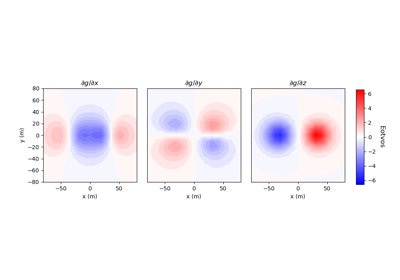
Forward Simulation of Gradiometry Data on a Tree Mesh
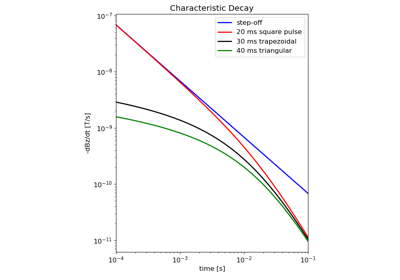
Response from a Homogeneous Layer for Different Waveforms

1D Forward Simulation with Chargeable and/or Magnetic Viscosity
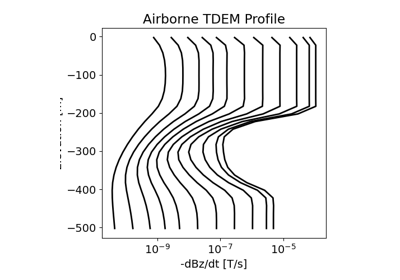
3D Forward Simulation for Transient Response on a Cylindrical Mesh
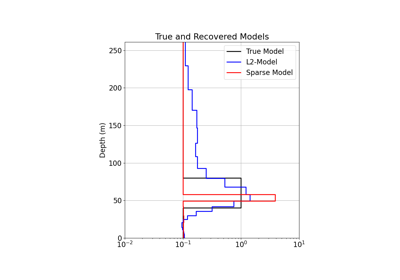
1D Inversion of Time-Domain Data for a Single Sounding
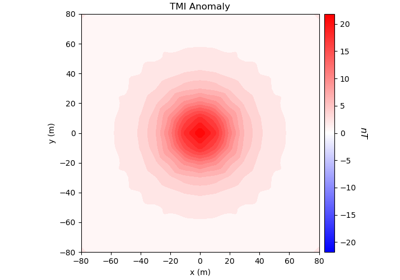
Forward Simulation of Total Magnetic Intensity Data
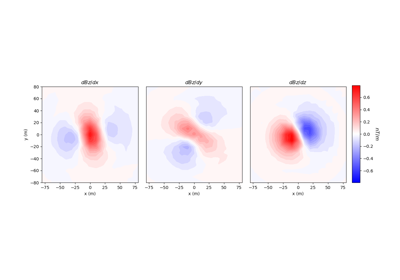
Forward Simulation of Gradiometry Data for Magnetic Vector Models
Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh