Note
Go to the end to download the full example code
3D Forward Simulation on a Tree Mesh#
Here we use the module SimPEG.electromagnetics.frequency_domain to simulate the FDEM response for an airborne survey using an OcTree mesh and a conductivity/resistivity model. To limit computational demant, we simulate airborne data at a single frequency for a vertical coplanar survey geometry. This tutorial can be easily adapted to simulate data at many frequencies. For this tutorial, we focus on the following:
How to define the transmitters and receivers
How to define the survey
How to define the topography
How to solve the FDEM problem on OcTree meshes
The units of the conductivity/resistivity model and resulting data
Please note that we have used a coarse mesh to shorten the time of the simulation. Proper discretization is required to simulate the fields at each frequency with sufficient accuracy.
Import modules#
from discretize import TreeMesh
from discretize.utils import mkvc, refine_tree_xyz, active_from_xyz
from SimPEG.utils import plot2Ddata
from SimPEG import maps
import SimPEG.electromagnetics.frequency_domain as fdem
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
try:
from pymatsolver import Pardiso as Solver
except ImportError:
from SimPEG import SolverLU as Solver
save_file = False
# sphinx_gallery_thumbnail_number = 2
Defining Topography#
Here we define surface topography as an (N, 3) numpy array. Topography could also be loaded from a file. Here we define flat topography, however more complex topographies can be considered.
Create Airborne Survey#
For this example, the survey consists of a uniform grid of airborne measurements. To save time, we will only compute the response for a single frequency.
# Frequencies being predicted
frequencies = [100, 500, 2500]
# Defining transmitter locations
N = 9
xtx, ytx, ztx = np.meshgrid(np.linspace(-200, 200, N), np.linspace(-200, 200, N), [40])
source_locations = np.c_[mkvc(xtx), mkvc(ytx), mkvc(ztx)]
ntx = np.size(xtx)
# Define receiver locations
xrx, yrx, zrx = np.meshgrid(np.linspace(-200, 200, N), np.linspace(-200, 200, N), [20])
receiver_locations = np.c_[mkvc(xrx), mkvc(yrx), mkvc(zrx)]
source_list = [] # Create empty list to store sources
# Each unique location and frequency defines a new transmitter
for ii in range(len(frequencies)):
for jj in range(ntx):
# Define receivers of different type at each location
bzr_receiver = fdem.receivers.PointMagneticFluxDensitySecondary(
receiver_locations[jj, :], "z", "real"
)
bzi_receiver = fdem.receivers.PointMagneticFluxDensitySecondary(
receiver_locations[jj, :], "z", "imag"
)
receivers_list = [bzr_receiver, bzi_receiver]
# Must define the transmitter properties and associated receivers
source_list.append(
fdem.sources.MagDipole(
receivers_list,
frequencies[ii],
source_locations[jj],
orientation="z",
moment=100,
)
)
survey = fdem.Survey(source_list)
Create OcTree Mesh#
Here we define the OcTree mesh that is used for this example. We chose to design a coarser mesh to decrease the run time. When designing a mesh to solve practical frequency domain problems:
Your smallest cell size should be 10%-20% the size of your smallest skin depth
The thickness of your padding needs to be 2-3 times biggest than your largest skin depth
The skin depth is ~500*np.sqrt(rho/f)
dh = 25.0 # base cell width
dom_width = 3000.0 # domain width
nbc = 2 ** int(np.round(np.log(dom_width / dh) / np.log(2.0))) # num. base cells
# Define the base mesh
h = [(dh, nbc)]
mesh = TreeMesh([h, h, h], x0="CCC")
# Mesh refinement based on topography
mesh = refine_tree_xyz(
mesh, topo_xyz, octree_levels=[0, 0, 0, 1], method="surface", finalize=False
)
# Mesh refinement near transmitters and receivers
mesh = refine_tree_xyz(
mesh, receiver_locations, octree_levels=[2, 4], method="radial", finalize=False
)
# Refine core mesh region
xp, yp, zp = np.meshgrid([-250.0, 250.0], [-250.0, 250.0], [-300.0, 0.0])
xyz = np.c_[mkvc(xp), mkvc(yp), mkvc(zp)]
mesh = refine_tree_xyz(mesh, xyz, octree_levels=[0, 2, 4], method="box", finalize=False)
mesh.finalize()
Defining the Conductivity/Resistivity Model and Mapping#
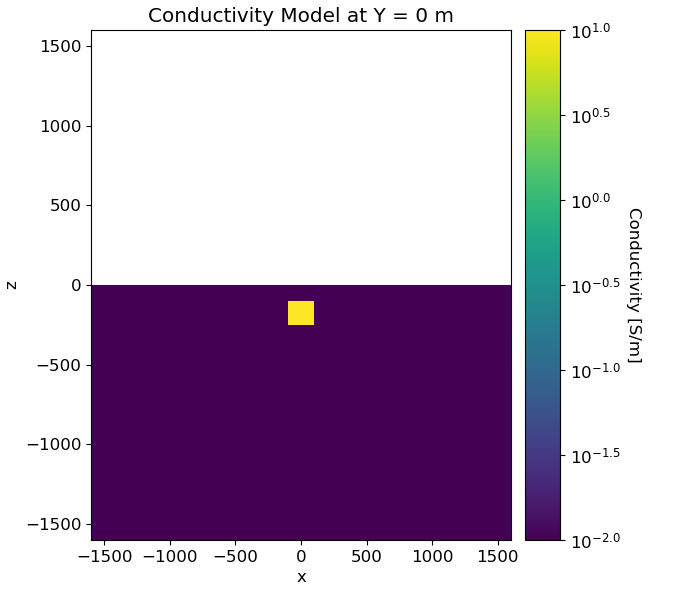
Here, we create the model that will be used to predict frequency domain data and the mapping from the model to the mesh. Here, the model consists of a conductive block within a more resistive background.
# Conductivity in S/m (or resistivity in Ohm m)
air_conductivity = 1e-8
background_conductivity = 1e-2
block_conductivity = 1e1
# Find cells that are active in the forward modeling (cells below surface)
ind_active = active_from_xyz(mesh, topo_xyz)
# Define mapping from model to active cells
model_map = maps.InjectActiveCells(mesh, ind_active, air_conductivity)
# Define model. Models in SimPEG are vector arrays
model = background_conductivity * np.ones(ind_active.sum())
ind_block = (
(mesh.gridCC[ind_active, 0] < 100.0)
& (mesh.gridCC[ind_active, 0] > -100.0)
& (mesh.gridCC[ind_active, 1] < 100.0)
& (mesh.gridCC[ind_active, 1] > -100.0)
& (mesh.gridCC[ind_active, 2] > -275.0)
& (mesh.gridCC[ind_active, 2] < -75.0)
)
model[ind_block] = block_conductivity
# Plot Resistivity Model
mpl.rcParams.update({"font.size": 12})
fig = plt.figure(figsize=(7, 6))
plotting_map = maps.InjectActiveCells(mesh, ind_active, np.nan)
log_model = np.log10(model)
ax1 = fig.add_axes([0.13, 0.1, 0.6, 0.85])
mesh.plot_slice(
plotting_map * log_model,
normal="Y",
ax=ax1,
ind=int(mesh.h[0].size / 2),
grid=False,
clim=(np.log10(background_conductivity), np.log10(block_conductivity)),
)
ax1.set_title("Conductivity Model at Y = 0 m")
ax2 = fig.add_axes([0.75, 0.1, 0.05, 0.85])
norm = mpl.colors.Normalize(
vmin=np.log10(background_conductivity), vmax=np.log10(block_conductivity)
)
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", format="$10^{%.1f}$"
)
cbar.set_label("Conductivity [S/m]", rotation=270, labelpad=15, size=12)
Simulation: Predicting FDEM Data#
Here we define the formulation for solving Maxwell’s equations. Since we are measuring the magnetic flux density and working with a conductivity model, the EB formulation is the most natural. We must also remember to define the mapping for the conductivity model. If you defined a resistivity model, use the kwarg rhoMap instead of sigmaMap
simulation = fdem.simulation.Simulation3DMagneticFluxDensity(
mesh, survey=survey, sigmaMap=model_map, solver=Solver
)
Predict and Plot Data#
Here we show how the simulation is used to predict data.
# Compute predicted data for a your model.
dpred = simulation.dpred(model)
# Data are organized by frequency, transmitter location, then by receiver. We nFreq transmitters
# and each transmitter had 2 receivers (real and imaginary component). So
# first we will pick out the real and imaginary data
bz_real = dpred[0 : len(dpred) : 2]
bz_imag = dpred[1 : len(dpred) : 2]
# Then we will will reshape the data for plotting.
bz_real_plotting = np.reshape(bz_real, (len(frequencies), ntx))
bz_imag_plotting = np.reshape(bz_imag, (len(frequencies), ntx))
fig = plt.figure(figsize=(10, 4))
# Real Component
frequencies_index = 0
v_max = np.max(np.abs(bz_real_plotting[frequencies_index, :]))
ax1 = fig.add_axes([0.05, 0.05, 0.35, 0.9])
plot2Ddata(
receiver_locations[:, 0:2],
bz_real_plotting[frequencies_index, :],
ax=ax1,
ncontour=30,
clim=(-v_max, v_max),
contourOpts={"cmap": "bwr"},
)
ax1.set_title("Re[$B_z$] at 100 Hz")
ax2 = fig.add_axes([0.41, 0.05, 0.02, 0.9])
norm = mpl.colors.Normalize(vmin=-v_max, vmax=v_max)
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", cmap=mpl.cm.bwr
)
cbar.set_label("$T$", rotation=270, labelpad=15, size=12)
# Imaginary Component
v_max = np.max(np.abs(bz_imag_plotting[frequencies_index, :]))
ax1 = fig.add_axes([0.55, 0.05, 0.35, 0.9])
plot2Ddata(
receiver_locations[:, 0:2],
bz_imag_plotting[frequencies_index, :],
ax=ax1,
ncontour=30,
clim=(-v_max, v_max),
contourOpts={"cmap": "bwr"},
)
ax1.set_title("Im[$B_z$] at 100 Hz")
ax2 = fig.add_axes([0.91, 0.05, 0.02, 0.9])
norm = mpl.colors.Normalize(vmin=-v_max, vmax=v_max)
cbar = mpl.colorbar.ColorbarBase(
ax2, norm=norm, orientation="vertical", cmap=mpl.cm.bwr
)
cbar.set_label("$T$", rotation=270, labelpad=15, size=12)
plt.show()
![Re[$B_z$] at 100 Hz, Im[$B_z$] at 100 Hz](../../../_images/sphx_glr_plot_fwd_3_fem_3d_002.png)
Optional: Export Data#
Write the true model, data and topography
if save_file:
dir_path = os.path.dirname(fdem.__file__).split(os.path.sep)[:-3]
dir_path.extend(["tutorials", "assets", "fdem"])
dir_path = os.path.sep.join(dir_path) + os.path.sep
# Write topography
fname = dir_path + "fdem_topo.txt"
np.savetxt(fname, np.c_[topo_xyz], fmt="%.4e")
# Write data with 2% noise added
fname = dir_path + "fdem_data.obs"
bz_real = bz_real + 1e-14 * np.random.rand(len(bz_real))
bz_imag = bz_imag + 1e-14 * np.random.rand(len(bz_imag))
f_vec = np.kron(frequencies, np.ones(ntx))
receiver_locations = np.kron(np.ones((len(frequencies), 1)), receiver_locations)
np.savetxt(fname, np.c_[f_vec, receiver_locations, bz_real, bz_imag], fmt="%.4e")
# Plot true model
output_model = plotting_map * model
output_model[np.isnan(output_model)] = 1e-8
fname = dir_path + "true_model.txt"
np.savetxt(fname, output_model, fmt="%.4e")
Total running time of the script: ( 0 minutes 19.215 seconds)
Estimated memory usage: 651 MB