Note
Go to the end to download the full example code
1D Inversion of for a Single Sounding#
Here we use the module SimPEG.electromangetics.frequency_domain_1d to invert frequency domain data and recover a 1D electrical conductivity model. In this tutorial, we focus on the following:
How to define sources and receivers from a survey file
How to define the survey
Sparse 1D inversion of with iteratively re-weighted least-squares
For this tutorial, we will invert 1D frequency domain data for a single sounding. The end product is layered Earth model which explains the data. The survey consisted of a vertical magnetic dipole source located 30 m above the surface. The receiver measured the vertical component of the secondary field at a 10 m offset from the source in ppm.
Import modules#
import os
import tarfile
import numpy as np
import matplotlib.pyplot as plt
from discretize import TensorMesh
import SimPEG.electromagnetics.frequency_domain as fdem
from SimPEG.utils import mkvc, plot_1d_layer_model
from SimPEG import (
maps,
data,
data_misfit,
inverse_problem,
regularization,
optimization,
directives,
inversion,
utils,
)
plt.rcParams.update({"font.size": 16, "lines.linewidth": 2, "lines.markersize": 8})
# sphinx_gallery_thumbnail_number = 2
Download Test Data File#
Here we provide the file path to the data we plan on inverting. The path to the data file is stored as a tar-file on our google cloud bucket: “https://storage.googleapis.com/simpeg/doc-assets/em1dfm.tar.gz”
# storage bucket where we have the data
data_source = "https://storage.googleapis.com/simpeg/doc-assets/em1dfm.tar.gz"
# download the data
downloaded_data = utils.download(data_source, overwrite=True)
# unzip the tarfile
tar = tarfile.open(downloaded_data, "r")
tar.extractall()
tar.close()
# path to the directory containing our data
dir_path = downloaded_data.split(".")[0] + os.path.sep
# files to work with
data_filename = dir_path + "em1dfm_data.txt"
Downloading https://storage.googleapis.com/simpeg/doc-assets/em1dfm.tar.gz
saved to: /home/vsts/work/1/s/tutorials/07-fdem/em1dfm.tar.gz
Download completed!
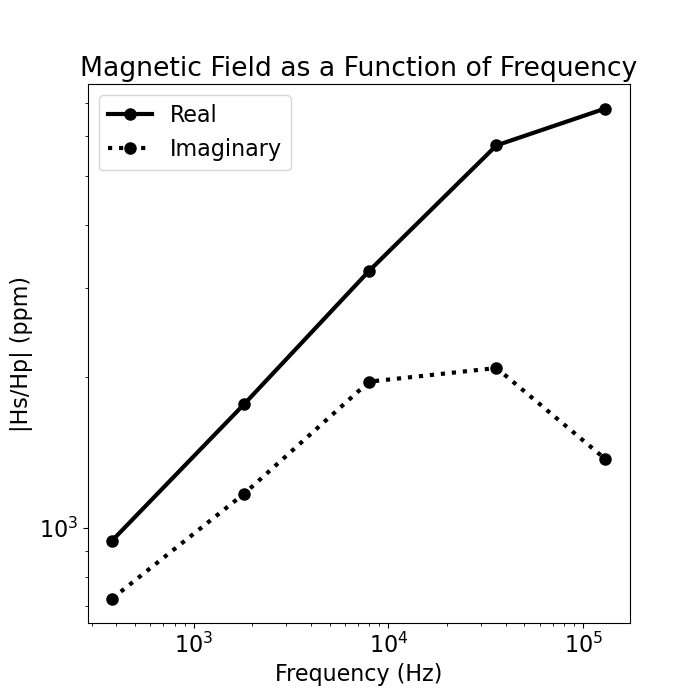
Load Data and Plot#
Here we load and plot the 1D sounding data. In this case, we have the secondary field response in ppm for a set of frequencies.
# Load field data
# dobs = np.loadtxt(str(data_filename))
dobs = np.loadtxt(str(data_filename), skiprows=1)
# Define receiver locations and observed data
frequencies = dobs[:, 0]
dobs = mkvc(dobs[:, 1:].T)
fig, ax = plt.subplots(1, 1, figsize=(7, 7))
ax.loglog(frequencies, np.abs(dobs[0::2]), "k-o", lw=3)
ax.loglog(frequencies, np.abs(dobs[1::2]), "k:o", lw=3)
ax.set_xlabel("Frequency (Hz)")
ax.set_ylabel("|Hs/Hp| (ppm)")
ax.set_title("Magnetic Field as a Function of Frequency")
ax.legend(["Real", "Imaginary"])
<matplotlib.legend.Legend object at 0x7f2dec65e9d0>
Defining the Survey#
Here we demonstrate a general way to define the receivers, sources and survey. The survey consisted of a vertical magnetic dipole source located 30 m above the surface. The receiver measured the vertical component of the secondary field at a 10 m offset from the source in ppm.
source_location = np.array([0.0, 0.0, 30.0])
moment = 1.0
receiver_location = np.array([10.0, 0.0, 30.0])
receiver_orientation = "z"
data_type = "ppm"
# Receiver list
receiver_list = []
receiver_list.append(
fdem.receivers.PointMagneticFieldSecondary(
receiver_location,
orientation=receiver_orientation,
data_type=data_type,
component="real",
)
)
receiver_list.append(
fdem.receivers.PointMagneticFieldSecondary(
receiver_location,
orientation=receiver_orientation,
data_type=data_type,
component="imag",
)
)
# Define source list
source_list = []
for freq in frequencies:
source_list.append(
fdem.sources.MagDipole(
receiver_list=receiver_list,
frequency=freq,
location=source_location,
orientation="z",
moment=moment,
)
)
# Survey
survey = fdem.survey.Survey(source_list)
Assign Uncertainties and Define the Data Object#
Here is where we define the data that are inverted. The data are defined by the survey, the observation values and the uncertainties.
# 5% of the absolute value
uncertainties = 0.05 * np.abs(dobs) * np.ones(np.shape(dobs))
# Define the data object
data_object = data.Data(survey, dobs=dobs, noise_floor=uncertainties)
Defining a 1D Layered Earth (1D Tensor Mesh)#
Here, we define the layer thicknesses for our 1D simulation. To do this, we use the TensorMesh class.
# Layer thicknesses
inv_thicknesses = np.logspace(0, 1.5, 25)
# Define a mesh for plotting and regularization.
mesh = TensorMesh([(np.r_[inv_thicknesses, inv_thicknesses[-1]])], "0")
Define a Starting and/or Reference Model and the Mapping#
Here, we create starting and/or reference models for the inversion as well as the mapping from the model space to the active cells. Starting and reference models can be a constant background value or contain a-priori structures. Here, the starting model is log(0.1) S/m.
Define log-conductivity values for each layer since our model is the log-conductivity. Don’t make the values 0! Otherwise the gradient for the 1st iteration is zero and the inversion will not converge.
# Define model. A resistivity (Ohm meters) or conductivity (S/m) for each layer.
starting_model = np.log(0.1 * np.ones(mesh.nC))
# Define mapping from model to active cells.
model_mapping = maps.ExpMap()
Define the Physics using a Simulation Object#
simulation = fdem.Simulation1DLayered(
survey=survey, thicknesses=inv_thicknesses, sigmaMap=model_mapping
)
Define Inverse Problem#
The inverse problem is defined by 3 things:
Data Misfit: a measure of how well our recovered model explains the field data
Regularization: constraints placed on the recovered model and a priori information
Optimization: the numerical approach used to solve the inverse problem
# Define the data misfit. Here the data misfit is the L2 norm of the weighted
# residual between the observed data and the data predicted for a given model.
# The weighting is defined by the reciprocal of the uncertainties.
dmis = data_misfit.L2DataMisfit(simulation=simulation, data=data_object)
# Define the regularization (model objective function)
reg_map = maps.IdentityMap(nP=mesh.nC)
reg = regularization.Sparse(mesh, mapping=reg_map, alpha_s=0.025, alpha_x=1.0)
# reference model
reg.mref = starting_model
# Define sparse and blocky norms p, q
reg.norms = [0, 0]
# Define how the optimization problem is solved. Here we will use an inexact
# Gauss-Newton approach that employs the conjugate gradient solver.
opt = optimization.ProjectedGNCG(maxIter=50, maxIterLS=20, maxIterCG=30, tolCG=1e-3)
# Define the inverse problem
inv_prob = inverse_problem.BaseInvProblem(dmis, reg, opt)
Define Inversion Directives#
Here we define any directiveas that are carried out during the inversion. This includes the cooling schedule for the trade-off parameter (beta), stopping criteria for the inversion and saving inversion results at each iteration.
# Defining a starting value for the trade-off parameter (beta) between the data
# misfit and the regularization.
starting_beta = directives.BetaEstimate_ByEig(beta0_ratio=1e1)
# Update the preconditionner
update_Jacobi = directives.UpdatePreconditioner()
# Options for outputting recovered models and predicted data for each beta.
save_iteration = directives.SaveOutputEveryIteration(save_txt=False)
# Directive for the IRLS
update_IRLS = directives.Update_IRLS(
max_irls_iterations=30, minGNiter=1, coolEpsFact=1.5, update_beta=True
)
# Updating the preconditionner if it is model dependent.
update_jacobi = directives.UpdatePreconditioner()
# Add sensitivity weights
sensitivity_weights = directives.UpdateSensitivityWeights()
# The directives are defined as a list.
directives_list = [
sensitivity_weights,
starting_beta,
save_iteration,
update_IRLS,
update_jacobi,
]
Running the Inversion#
To define the inversion object, we need to define the inversion problem and the set of directives. We can then run the inversion.
# Here we combine the inverse problem and the set of directives
inv = inversion.BaseInversion(inv_prob, directives_list)
# Run the inversion
recovered_model = inv.run(starting_model)
SimPEG.InvProblem is setting bfgsH0 to the inverse of the eval2Deriv.
***Done using same Solver, and solver_opts as the Simulation1DLayered problem***
model has any nan: 0
=============================== Projected GNCG ===============================
# beta phi_d phi_m f |proj(x-g)-x| LS Comment
-----------------------------------------------------------------------------
x0 has any nan: 0
0 2.46e+02 1.40e+02 0.00e+00 1.40e+02 3.95e+01 0
1 1.23e+02 2.15e+01 1.09e-01 3.50e+01 1.84e+01 0
Reached starting chifact with l2-norm regularization: Start IRLS steps...
irls_threshold 2.730172413633053
2 6.16e+01 3.89e+00 1.13e-01 1.09e+01 4.99e+00 0
3 1.32e+02 2.20e+00 1.20e-01 1.80e+01 8.22e+00 0 Skip BFGS
4 2.10e+02 4.22e+00 9.35e-02 2.38e+01 1.03e+01 0
5 1.57e+02 6.71e+00 7.95e-02 1.92e+01 2.79e+00 0
6 1.15e+02 6.93e+00 7.99e-02 1.61e+01 1.82e+00 0 Skip BFGS
7 8.79e+01 6.45e+00 7.75e-02 1.33e+01 1.88e+00 0
8 7.14e+01 5.72e+00 6.99e-02 1.07e+01 1.96e+00 0
9 7.14e+01 4.89e+00 6.23e-02 9.33e+00 3.12e+00 0
10 1.12e+02 4.43e+00 4.93e-02 9.94e+00 9.42e+00 0
11 1.12e+02 4.70e+00 3.40e-02 8.50e+00 6.64e+00 0
12 1.12e+02 4.59e+00 2.39e-02 7.25e+00 6.78e+00 0 Skip BFGS
13 1.77e+02 4.25e+00 1.73e-02 7.33e+00 1.74e+01 0
14 2.83e+02 4.21e+00 1.16e-02 7.49e+00 2.22e+01 0
15 4.49e+02 4.23e+00 7.73e-03 7.71e+00 2.04e+01 0
16 7.12e+02 4.27e+00 5.11e-03 7.91e+00 2.78e+01 0
17 1.13e+03 4.31e+00 3.30e-03 8.03e+00 2.04e+01 0
18 1.77e+03 4.35e+00 2.17e-03 8.20e+00 1.63e+01 0 Skip BFGS
19 2.78e+03 4.40e+00 1.43e-03 8.37e+00 1.62e+01 0 Skip BFGS
20 4.35e+03 4.44e+00 9.41e-04 8.53e+00 1.61e+01 0
21 6.77e+03 4.49e+00 6.19e-04 8.68e+00 1.60e+01 0
22 6.77e+03 4.54e+00 4.07e-04 7.29e+00 6.25e+00 0 Skip BFGS
23 1.07e+04 4.32e+00 2.89e-04 7.40e+00 1.74e+01 0
24 1.69e+04 4.27e+00 1.95e-04 7.58e+00 1.67e+01 0 Skip BFGS
25 2.69e+04 4.27e+00 1.30e-04 7.77e+00 1.65e+01 0 Skip BFGS
26 4.25e+04 4.30e+00 8.62e-05 7.96e+00 1.63e+01 0
27 6.70e+04 4.34e+00 5.68e-05 8.14e+00 1.62e+01 0
28 1.05e+05 4.38e+00 3.74e-05 8.31e+00 1.62e+01 0
29 1.65e+05 4.43e+00 2.46e-05 8.48e+00 1.61e+01 0
30 2.57e+05 4.47e+00 1.62e-05 8.63e+00 1.60e+01 0
31 2.57e+05 4.52e+00 1.06e-05 7.25e+00 6.24e+00 0 Skip BFGS
Reach maximum number of IRLS cycles: 30
------------------------- STOP! -------------------------
1 : |fc-fOld| = 0.0000e+00 <= tolF*(1+|f0|) = 1.4148e+01
1 : |xc-x_last| = 1.2995e-01 <= tolX*(1+|x0|) = 1.2741e+00
0 : |proj(x-g)-x| = 6.2373e+00 <= tolG = 1.0000e-01
0 : |proj(x-g)-x| = 6.2373e+00 <= 1e3*eps = 1.0000e-02
0 : maxIter = 50 <= iter = 32
------------------------- DONE! -------------------------
Plotting Results#
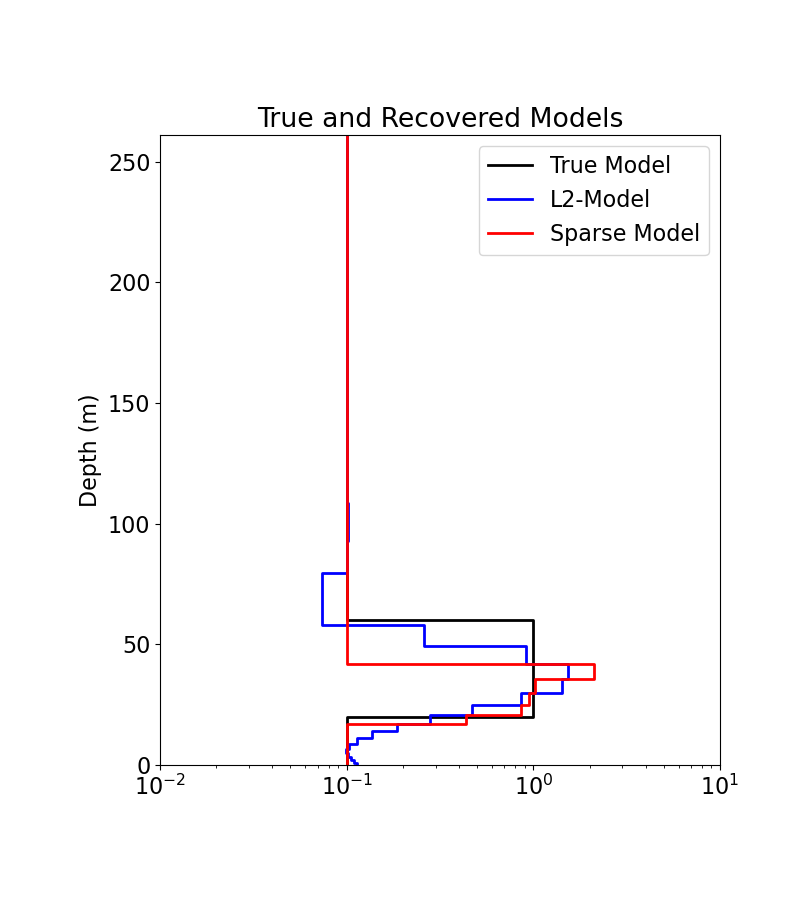
# Load the true model and layer thicknesses
true_model = np.array([0.1, 1.0, 0.1])
true_layers = np.r_[20.0, 40.0, 160.0]
# Extract Least-Squares model
l2_model = inv_prob.l2model
# Plot true model and recovered model
fig = plt.figure(figsize=(8, 9))
x_min = np.min(
np.r_[model_mapping * recovered_model, model_mapping * l2_model, true_model]
)
x_max = np.max(
np.r_[model_mapping * recovered_model, model_mapping * l2_model, true_model]
)
ax1 = fig.add_axes([0.2, 0.15, 0.7, 0.7])
plot_1d_layer_model(true_layers, true_model, ax=ax1, show_layers=False, color="k")
plot_1d_layer_model(
mesh.h[0], model_mapping * l2_model, ax=ax1, show_layers=False, color="b"
)
plot_1d_layer_model(
mesh.h[0], model_mapping * recovered_model, ax=ax1, show_layers=False, color="r"
)
ax1.set_xlim(0.01, 10)
ax1.set_title("True and Recovered Models")
ax1.legend(["True Model", "L2-Model", "Sparse Model"])
plt.gca().invert_yaxis()
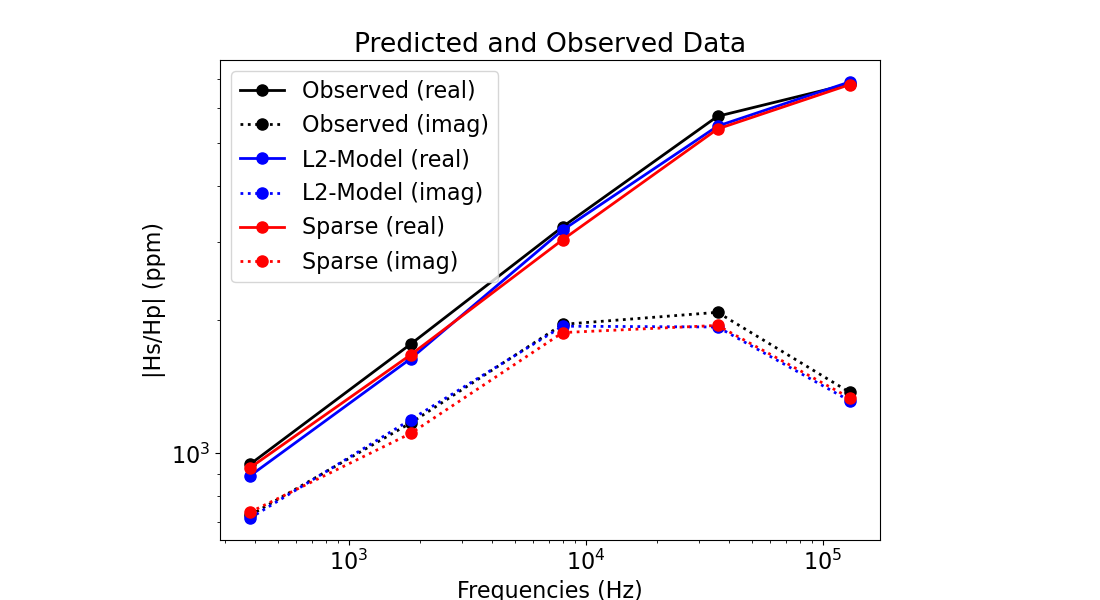
# Plot predicted and observed data
dpred_l2 = simulation.dpred(l2_model)
dpred_final = simulation.dpred(recovered_model)
fig = plt.figure(figsize=(11, 6))
ax1 = fig.add_axes([0.2, 0.1, 0.6, 0.8])
ax1.loglog(frequencies, np.abs(dobs[0::2]), "k-o")
ax1.loglog(frequencies, np.abs(dobs[1::2]), "k:o")
ax1.loglog(frequencies, np.abs(dpred_l2[0::2]), "b-o")
ax1.loglog(frequencies, np.abs(dpred_l2[1::2]), "b:o")
ax1.loglog(frequencies, np.abs(dpred_final[0::2]), "r-o")
ax1.loglog(frequencies, np.abs(dpred_final[1::2]), "r:o")
ax1.set_xlabel("Frequencies (Hz)")
ax1.set_ylabel("|Hs/Hp| (ppm)")
ax1.set_title("Predicted and Observed Data")
ax1.legend(
[
"Observed (real)",
"Observed (imag)",
"L2-Model (real)",
"L2-Model (imag)",
"Sparse (real)",
"Sparse (imag)",
],
loc="upper left",
)
plt.show()
Total running time of the script: ( 0 minutes 27.719 seconds)
Estimated memory usage: 17 MB