simpeg.maps.ParametricSplineMap#

class simpeg.maps.ParametricSplineMap(mesh, pts, ptsv=None, order=3, logSigma=True, normal='x', slope=10000.0)[source]#

Bases: IdentityMap

Mapping to parameterize the boundary between two geological units using spline interpolation.

$$g=f(x)-y$$

Define the model as:

$$m=[{\sigma }_1,{\sigma }_2,y]$$

Parameters:

meshdiscretize.BaseMesh

A discretize mesh

pts(n) numpy.ndarray

Points for the 1D spline tie points.

ptsv(2) array_like

Points for linear interpolation between two splines in 3D.

orderint

Order of the spline mapping; e.g. 3 is cubic spline

logSigmabool

If True, ${\sigma }_1$ and ${\sigma }_2$ represent the natural log of some physical property value for each unit.

normal{‘x’, ‘y’, ‘z’}

Defines the general direction of the normal vector for the interface.

slopefloat

Parameter for defining the sharpness of the boundary. The sharpness is increased if slope is large.

Attributes

is_linear	Determine whether or not this mapping is a linear operation.
logSigma	Whether the input needs to be transformed by an exponential
mesh	The mesh used for the mapping
nP	Number of parameters the mapping acts on
normal	The projection axis.
npts	The number of points.
order	Order of the spline mapping.
pts	Points for the spline.
ptsv	Bottom and top values for the 3D spline surface.
shape	Dimensions of the mapping operator
slope	Sharpness of the boundary.

Methods

deriv(m[, v])	Derivative of the mapping with respect to the input parameters.
dot(map1)	Multiply two mappings to create a simpeg.maps.ComboMap.
inverse(D)	The transform inverse is not implemented.
test([m, num, random_seed])	Derivative test for the mapping.

Examples

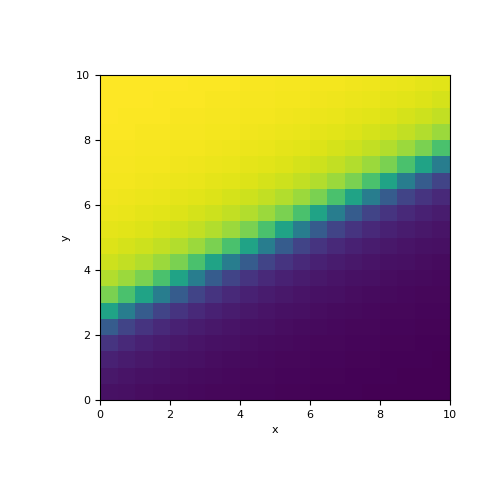
In this example, we define a 2 layered model with a sloping interface on a 2D mesh. The model consists of the physical property values for the layers and the known elevations for the interface at the horizontal positions supplied when creating the mapping.

>>> from simpeg.maps import ParametricSplineMap
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt

>>> h = 0.5*np.ones(20)
>>> mesh = TensorMesh([h, h])

>>> x = np.linspace(0, 10, 6)
>>> y = 0.5*x + 2.5

>>> model = np.r_[10., 0., y]
>>> mapping = ParametricSplineMap(mesh, x, order=2, normal='Y', slope=2)

>>> fig = plt.figure(figsize=(5, 5))
>>> ax = fig.add_subplot(111)
>>> mesh.plot_image(mapping * model, ax=ax)

(Source code, png, pdf)