simpeg.objective_function.BaseObjectiveFunction#

class simpeg.objective_function.BaseObjectiveFunction(nP=None, mapping=None, has_fields=False, counter=None, debug=False)[source]#

Bases: BaseSimPEG

Base class for creating objective functions.

The BaseObjectiveFunction class defines properties and methods inherited by other classes in SimPEG that represent objective functions; e.g. regularization, data misfit. These include convenient methods for testing the order of convergence and ajoint operations.

Important

This class is not meant to be instantiated. You should inherit from it to create your own objective function class.

Important

If building a regularization function within SimPEG, please inherit simpeg.regularization.BaseRegularization, as this class has additional functionality related to regularization. And if building a data misfit function, please inherit simpeg.data_misfit.BaseDataMisfit.

Parameters:

nPint: Number of model parameters.
mappingsimpeg.mapping.BaseMap: A SimPEG mapping object that maps from the model space to the quantity evaluated in the objective function.
has_fieldsbool: If True, predicted fields for a simulation and a given model can be used to evaluate the objective function quickly.
counterNone or simpeg.utils.Counter: Assign a SimPEG Counter object to store iterations and run-times.
debugbool: Print debugging information.

Attributes

`mapping`	Mapping from the model to the quantity evaluated in the object function.
`nP`	Number of model parameters.

Methods

`__call__`(x[, f])	Evaluate the objective function for a given model.
`deriv`(m, **kwargs)	Gradient of the objective function evaluated for the model provided.
`deriv2`(m[, v])	Hessian of the objective function evaluated for the model provided.
`map_class`	Base class of expected maps.
`test`([x, num, random_seed])	Run a convergence test on both the first and second derivatives.

Galleries and Tutorials using `simpeg.objective_function.BaseObjectiveFunction`#

Maps: ComboMaps

PF: Gravity: Tiled Inversion Linear

Magnetic inversion on a TreeMesh with remanence

Magnetic inversion on a TreeMesh

Magnetic Amplitude inversion on a TreeMesh

3D DC inversion of Dipole Dipole array

Parametric DC inversion with Dipole Dipole array

2D inversion of Loop-Loop EM Data

EM: TDEM: 1D: Inversion

EM: TDEM: 1D: Inversion with VTEM waveform

Method of Equivalent Sources for Removing VRM Responses

FLOW: Richards: 1D: Inversion

Petrophysically guided inversion (PGI): Linear example

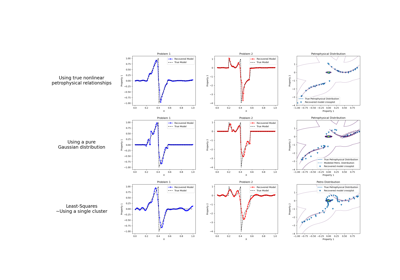
Petrophysically guided inversion: Joint linear example with nonlinear relationships

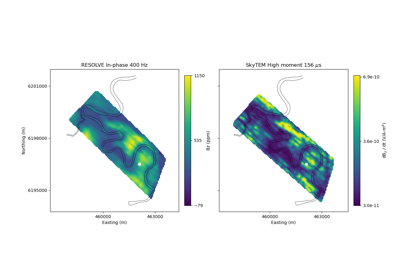
Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions

Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion

Heagy et al., 2017 1D FDEM and TDEM inversions

PF: Gravity: Laguna del Maule Bouguer Gravity

Straight Ray with Volume Data Misfit Term

Linear Least-Squares Inversion

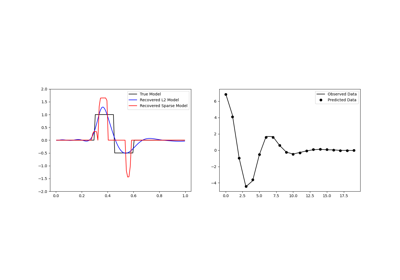
Sparse Inversion with Iteratively Re-Weighted Least-Squares

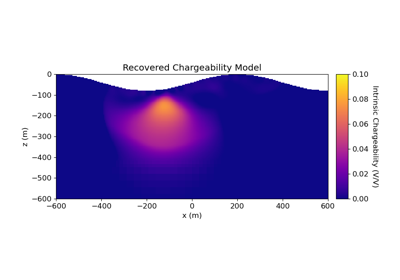
2.5D DC Resistivity and IP Least-Squares Inversion

3D Least-Squares Inversion of DC and IP Data

1D Inversion of for a Single Sounding

1D Inversion of Time-Domain Data for a Single Sounding

Sparse Norm Inversion of 2D Seismic Tomography Data

Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data

Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information

simpeg.objective_function.BaseObjectiveFunction#

Galleries and Tutorials using simpeg.objective_function.BaseObjectiveFunction#

This Page

Galleries and Tutorials using `simpeg.objective_function.BaseObjectiveFunction`#