SimPEG.regularization.Sparse

class SimPEG.regularization.Sparse(mesh, active_cells=None, norms=None, gradient_type='total', irls_scaled=True, irls_threshold=1e-08, **kwargs)

Bases: SimPEG.regularization.base.WeightedLeastSquares

The regularization is:

$$R(m)=\frac{1}{2}\mathbf{(}\mathbf{m}\mathbf{-}{\mathbf{m}}_{\mathbf{\text{ref}}}{\mathbf{)}}^{\mathrm{\top }}{\mathbf{W}}^{\mathrm{\top }}{\mathbf{R}}^{\mathrm{\top }}\mathbf{R}\mathbf{W}\mathbf{(}\mathbf{m}\mathbf{-}{\mathbf{m}}_{\mathbf{\text{ref}}}\mathbf{)}$$

where the IRLS weight

$$R=\eta \text{diag}{\left[{\mathbf{r}}_s\right]}^{1/2}{r}_{s_i}={({({m_i}^{(k-1)})}^2+{ϵ}^2)}^{p_s/2-1}$$

where k denotes the iteration number. So the derivative is straight forward:

$$R(m)={\mathbf{W}}^{\mathrm{\top }}{\mathbf{R}}^{\mathrm{\top }}\mathbf{R}\mathbf{W}\mathbf{(}\mathbf{m}\mathbf{-}{\mathbf{m}}_{\mathbf{\text{ref}}}\mathbf{)}$$

The IRLS weights are re-computed after each beta solves using Update_IRLS within the inversion directives.

Attributes

gradientType	0.gradientType has been deprecated.
gradient_type	Choice of gradient measure used in the irls weights
irls_scaled	Scale irls weights.
irls_threshold	Constant added to the denominator of the IRLS weights for stability.
norms	Value of the norm

Methods

update_weights(model)

Trigger irls update on all children

Galleries and Tutorials using SimPEG.regularization.Sparse

Maps: ComboMaps

Maps: ComboMaps

PF: Gravity: Tiled Inversion Linear

PF: Gravity: Tiled Inversion Linear

Magnetic inversion on a TreeMesh

Magnetic inversion on a TreeMesh

Magnetic Amplitude inversion on a TreeMesh

Magnetic Amplitude inversion on a TreeMesh

PF: Gravity: Laguna del Maule Bouguer Gravity

PF: Gravity: Laguna del Maule Bouguer Gravity

1D Inversion of for a Single Sounding

1D Inversion of for a Single Sounding

Sparse Norm Inversion of Gravity Anomaly Data

Sparse Norm Inversion of Gravity Anomaly Data

Sparse 1D Inversion of Sounding Data

Sparse 1D Inversion of Sounding Data

2.5D DC Resistivity Inversion with Sparse Norms

2.5D DC Resistivity Inversion with Sparse Norms

Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh

Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh

Sparse Norm Inversion of 2D Seismic Tomography Data

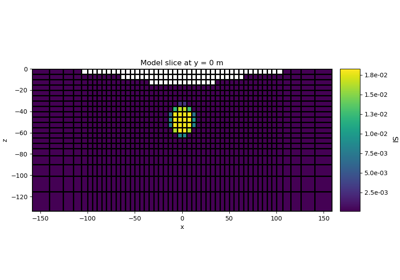
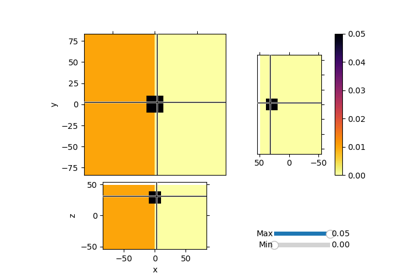
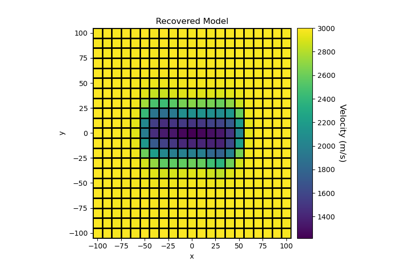
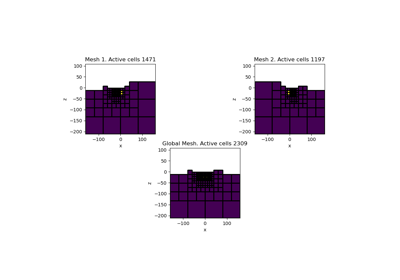
Sparse Norm Inversion of 2D Seismic Tomography Data

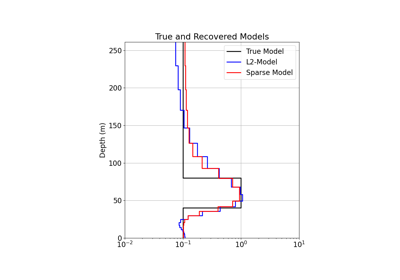
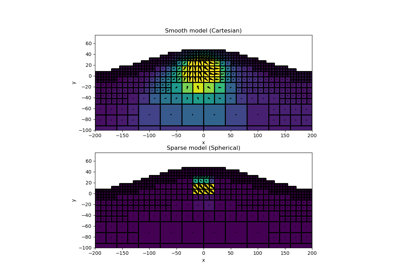
1D Inversion of Time-Domain Data for a Single Sounding

1D Inversion of Time-Domain Data for a Single Sounding

Sparse Inversion with Iteratively Re-Weighted Least-Squares

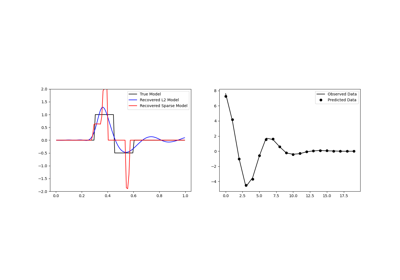
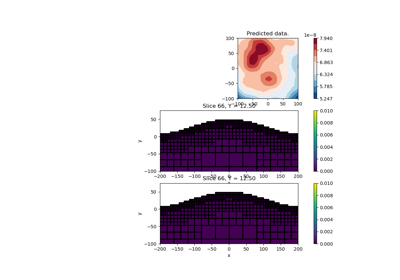
Sparse Inversion with Iteratively Re-Weighted Least-Squares