Note
Click here to download the full example code
Simulate a 1D Sounding over a Layered Earth#
Here we use the module SimPEG.electromangetics.static.resistivity to predict sounding data over a 1D layered Earth. In this tutorial, we focus on the following:
General definition of sources and receivers
How to define the survey
How to predict voltage or apparent resistivity data
The units of the model and resulting data
For this tutorial, we will simulate sounding data over a layered Earth using a Wenner array. The end product is a sounding curve which tells us how the electrical resistivity changes with depth.
Import modules#
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from SimPEG import maps
from SimPEG.electromagnetics.static import resistivity as dc
from SimPEG.utils import plot_1d_layer_model
mpl.rcParams.update({"font.size": 16})
write_output = False
# sphinx_gallery_thumbnail_number = 2
Create Survey#
Here we demonstrate a general way to define sources and receivers. For pole and dipole sources, we must define the A or AB electrode locations, respectively. For the pole and dipole receivers, we must define the M or MN electrode locations, respectively.
a_min = 20.0
a_max = 500.0
n_stations = 25
# Define the 'a' spacing for Wenner array measurements for each reading
electrode_separations = np.linspace(a_min, a_max, n_stations)
source_list = [] # create empty array for sources to live
for ii in range(0, len(electrode_separations)):
# Extract separation parameter for sources and receivers
a = electrode_separations[ii]
# AB electrode locations for source. Each is a (1, 3) numpy array
A_location = np.r_[-1.5 * a, 0.0, 0.0]
B_location = np.r_[1.5 * a, 0.0, 0.0]
# MN electrode locations for receivers. Each is an (N, 3) numpy array
M_location = np.r_[-0.5 * a, 0.0, 0.0]
N_location = np.r_[0.5 * a, 0.0, 0.0]
# Create receivers list. Define as pole or dipole.
receiver_list = dc.receivers.Dipole(M_location, N_location)
receiver_list = [receiver_list]
# Define the source properties and associated receivers
source_list.append(dc.sources.Dipole(receiver_list, A_location, B_location))
# Define survey
survey = dc.Survey(source_list)
Defining a 1D Layered Earth Model#
Here, we define the layer thicknesses and electrical resistivities for our 1D simulation. If we have N layers, we define N electrical resistivity values and N-1 layer thicknesses. The lowest layer is assumed to extend to infinity. In the case of a halfspace, the layer thicknesses would be an empty array.
# Define layer thicknesses.
layer_thicknesses = np.r_[100.0, 100.0]
# Define layer resistivities.
model = np.r_[1e3, 4e3, 2e2]
# Define mapping from model to 1D layers.
model_map = maps.IdentityMap(nP=len(model))
Plot Resistivity Model#
Here we plot the 1D resistivity model.
# Plot the 1D model
ax = plot_1d_layer_model(layer_thicknesses, model_map * model)
ax.set_xlabel(r"Resistivity ($\Omega m$)")
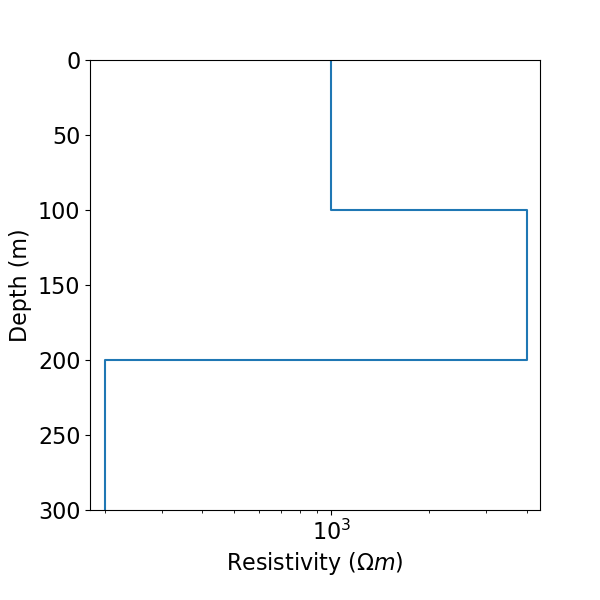
Text(0.5, 49.52222222222221, 'Resistivity ($\\Omega m$)')
Define the Forward Simulation and Predict DC Resistivity Data#
Here we predict DC resistivity data. If the keyword argument rhoMap is defined, the simulation will expect a resistivity model. If the keyword argument sigmaMap is defined, the simulation will expect a conductivity model.
simulation = dc.simulation_1d.Simulation1DLayers(
survey=survey,
rhoMap=model_map,
thicknesses=layer_thicknesses,
data_type="apparent_resistivity",
)
# Predict data for a given model
dpred = simulation.dpred(model)
# Plot apparent resistivities on sounding curve
fig = plt.figure(figsize=(11, 5))
ax1 = fig.add_axes([0.1, 0.1, 0.75, 0.85])
ax1.semilogy(1.5 * electrode_separations, dpred, "b")
ax1.set_xlabel("AB/2 (m)")
ax1.set_ylabel(r"Apparent Resistivity ($\Omega m$)")
plt.show()
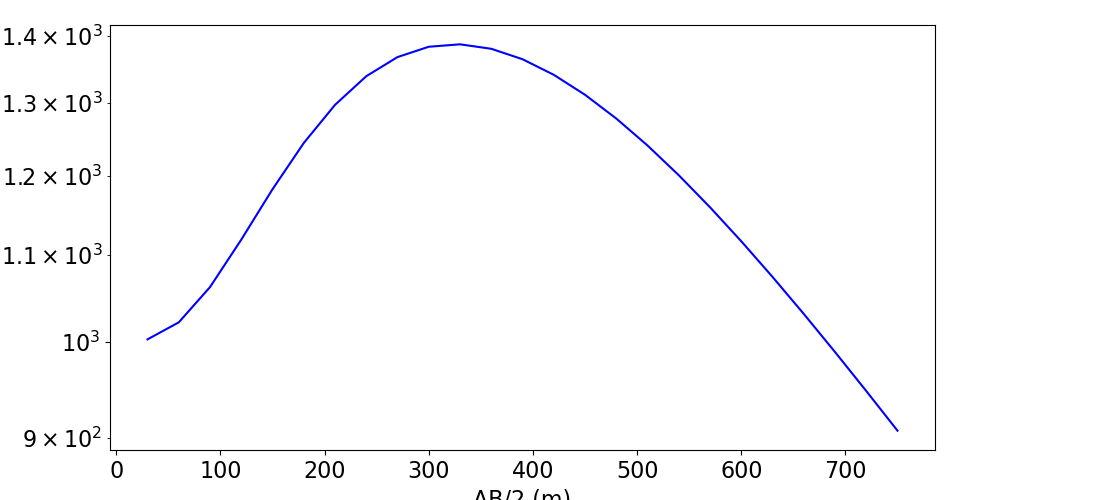
Optional: Export Data#
Export data and true model
if write_output:
dir_path = os.path.dirname(__file__).split(os.path.sep)
dir_path.extend(["outputs"])
dir_path = os.path.sep.join(dir_path) + os.path.sep
if not os.path.exists(dir_path):
os.mkdir(dir_path)
np.random.seed(145)
noise = 0.025 * dpred * np.random.rand(len(dpred))
data_array = np.c_[
survey.locations_a,
survey.locations_b,
survey.locations_m,
survey.locations_n,
dpred + noise,
]
fname = dir_path + "app_res_1d_data.dobs"
np.savetxt(fname, data_array, fmt="%.4e")
Total running time of the script: ( 0 minutes 3.209 seconds)
Estimated memory usage: 18 MB