SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity#
- class SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity(mesh, survey=None, dt_threshold=1e-08, **kwargs)[source]#
Bases:
BaseTDEMSimulationStarting from the quasi-static E-B formulation of Maxwell’s equations (semi-discretized)
\[\begin{split}\mathbf{C} \mathbf{e} + \frac{\partial \mathbf{b}}{\partial t} = \mathbf{s_m} \\ \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e} \mathbf{e} = \mathbf{s_e}\end{split}\]where \(\mathbf{s_e}\) is an integrated quantity, we eliminate \(\mathbf{e}\) using
\[\mathbf{e} = \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}\]to obtain a second order semi-discretized system in \(\mathbf{b}\)
\[\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} + \frac{\partial \mathbf{b}}{\partial t} = \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e} + \mathbf{s_m}\]and moving everything except the time derivative to the rhs gives
\[\frac{\partial \mathbf{b}}{\partial t} = -\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} + \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e} + \mathbf{s_m}\]For the time discretization, we use backward euler. To solve for the \(n+1\) th time step, we have
\[\frac{\mathbf{b}^{n+1} - \mathbf{b}^{n}}{\mathbf{dt}} = -\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b}^{n+1} + \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}^{n+1} + \mathbf{s_m}^{n+1}\]re-arranging to put \(\mathbf{b}^{n+1}\) on the left hand side gives
\[(\mathbf{I} + \mathbf{dt} \mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f}) \mathbf{b}^{n+1} = \mathbf{b}^{n} + \mathbf{dt}(\mathbf{C} \mathbf{M_{\sigma}^e}^{-1} \mathbf{s_e}^{n+1} + \mathbf{s_m}^{n+1})\]Methods
Fields_Derivsalias of
FieldsDerivativesEBfieldsPairalias of
Fields3DMagneticFluxDensitygetAdiag(tInd)System matrix at a given time index
getAdiagDeriv(tInd, u, v[, adjoint])Derivative of ADiag
getAsubdiag(tInd)Matrix below the diagonal
getRHS(tInd)Assemble the RHS
getRHSDeriv(tInd, src, v[, adjoint])Derivative of the RHS
getAsubdiagDeriv
Galleries and Tutorials using SimPEG.electromagnetics.time_domain.Simulation3DMagneticFluxDensity#
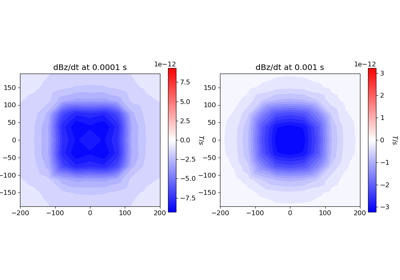
3D Forward Simulation for Transient Response on a Cylindrical Mesh