SimPEG.maps.ParametricLayer

class SimPEG.maps.ParametricLayer(mesh, **kwargs)

Bases: BaseParametric

Mapping for a horizontal layer within a wholespace.

This mapping is used when the cells lying below the Earth’s surface can be parameterized by horizontal layer within a homogeneous medium. The model is defined by the physical property value for the background (\(\sigma_0\)), the physical property value for the layer (\(\sigma_1\)), the elevation for the middle of the layer (\(z_L\)) and the thickness of the layer \(h\).

For this mapping, the set of input model parameters are organized:

\[\mathbf{m} = [\sigma_0, \;\sigma_1,\; z_L , \; h]\]

The mapping \(\mathbf{u}(\mathbf{m})\) from the model to the mesh is given by:

\[\mathbf{u}(\mathbf{m}) = \sigma_0 + \frac{(\sigma_1 - \sigma_0)}{\pi} \Bigg [ \arctan \Bigg ( a \bigg ( \mathbf{z_c} - z_L + \frac{h}{2} \bigg ) \Bigg ) - \arctan \Bigg ( a \bigg ( \mathbf{z_c} - z_L - \frac{h}{2} \bigg ) \Bigg ) \Bigg ]\]

where \(\mathbf{z_c}\) is a vectors containing the vertical cell center locations for all active cells in the mesh, and \(a\) is a parameter which defines the sharpness of the boundaries between the layer and the background.

Parameters:

meshdiscretize.BaseMesh

A discretize mesh

indActivenumpy.ndarray

Active cells array. Can be a boolean numpy.ndarray of length mesh.nC or a numpy.ndarray of int containing the indices of the active cells.

slopefloat

Directly define the constant a in the mapping function which defines the sharpness of the boundaries.

slopeFactfloat

Scaling factor for the sharpness of the boundaries based on cell size. Using this option, we set a = slopeFact / dh.

Examples

In this example, we define a layer in a wholespace whose interface is sharp. We construct the mapping from the model to the set of active cells (i.e. below the surface), We then use an active cells mapping to map from the set of active cells to all cells in the mesh.

>>> from SimPEG.maps import ParametricLayer, InjectActiveCells
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt

>>> dh = 0.25*np.ones(40)
>>> mesh = TensorMesh([dh, dh])
>>> ind_active = mesh.cell_centers[:, 1] < 8

>>> sig0, sig1, zL, h = 5., 10., 4., 2
>>> model = np.r_[sig0, sig1, zL, h]

>>> layer_map = ParametricLayer(
>>>     mesh, indActive=ind_active, slope=4
>>> )
>>> act_map = InjectActiveCells(mesh, ind_active, 0.)

>>> fig = plt.figure(figsize=(5, 5))
>>> ax = fig.add_subplot(111)
>>> mesh.plot_image(act_map * layer_map * model, ax=ax)

(Source code, png, pdf)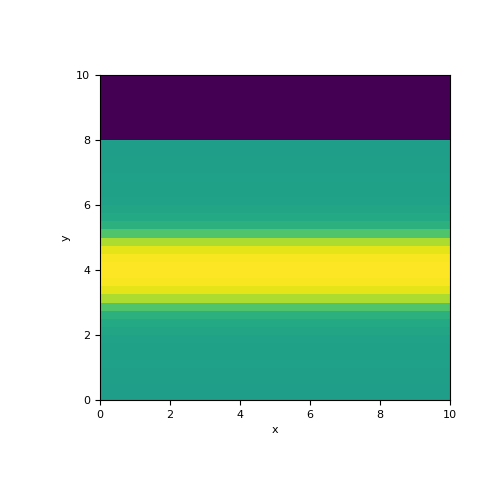

Attributes

nP	Number of model parameters the mapping acts on; i.e 4
shape	Dimensions of the mapping

Methods

deriv(m)	Derivative of the mapping with respect to the input parameters.
mDict(m)	Return model parameters as a dictionary.

layer_cont

Galleries and Tutorials using SimPEG.maps.ParametricLayer

Maps: Parametric Block in a Layer

Maps: Parametric Block in a Layer

Maps: Parametrized Layer

Maps: Parametrized Layer

Heagy et al., 2017 Casing Example

Heagy et al., 2017 Casing Example