simpeg.regularization.Sparse#
- class simpeg.regularization.Sparse(mesh, active_cells=None, norms=None, gradient_type='total', irls_scaled=True, irls_threshold=1e-08, objfcts=None, **kwargs)[source]#
Bases:
WeightedLeastSquaresSparse norm weighted least squares regularization.
Apply regularization for recovering compact and/or blocky structures using a weighted sum of
SparseSmallnessandSparseSmoothnessregularization functions. The level of compactness and blockiness is controlled by the norms within the respective regularization functions; with more sparse structures (compact and/or blocky) being recovered when smaller norms are used. Optionally, custom cell weights can be applied to control the degree of sparseness being enforced throughout different regions the model.See the Notes section below for a comprehensive description.
- Parameters:
- mesh
simpeg.regularization.RegularizationMesh,discretize.base.BaseMesh Mesh on which the regularization is discretized. This is not necessarily the same as the mesh on which the simulation is defined.
- active_cells
None, (n_cells, )numpy.ndarrayofbool Boolean array defining the set of
RegularizationMeshcells that are active in the inversion. IfNone, all cells are active.- mapping
None,simpeg.maps.BaseMap The mapping from the model parameters to the active cells in the inversion. If
None, the mapping is the identity map.- reference_model
None, (n_param, )numpy.ndarray Reference model. If
None, the reference model in the inversion is set to the starting model.- reference_model_in_smoothbool,
optional Whether to include the reference model in the smoothness terms.
- units
None,str Units for the model parameters. Some regularization classes behave differently depending on the units; e.g. ‘radian’.
- weights
None,dict Weight multipliers to customize the least-squares function. Each key points to a (n_cells, ) numpy.ndarray that is defined on the
RegularizationMesh.- alpha_s
float,optional Scaling constant for the smallness regularization term.
- alpha_x, alpha_y, alpha_z
floatorNone,optional Scaling constants for the first order smoothness along x, y and z, respectively. If set to
None, the scaling constant is set automatically according to the value of the length_scale parameter.- length_scale_x, length_scale_y, length_scale_z
float,optional First order smoothness length scales for the respective dimensions.
- gradient_type{“total”, “component”}
Gradient measure used in the IRLS re-weighting. Whether to re-weight using the total gradient or components of the gradient.
- norms(dim+1, )
numpy.ndarray The respective norms used for the sparse smallness, x-smoothness, (y-smoothness and z-smoothness) regularization function. Must all be within the interval [0, 2]. E.g. np.r_[2, 1, 1, 1] uses a 2-norm on the smallness term and a 1-norm on all smoothness terms.
- irls_scaledbool
If
True, scale the IRLS weights to preserve magnitude of the regularization function. IfFalse, do not scale.- irls_threshold
float Constant added to IRLS weights to ensures stability in the algorithm.
- mesh
Attributes
Full weighting matrix for the combo objective function.
Active cells defined on the regularization mesh.
Multiplier constant for the smallness term.
Multiplier constant for first-order smoothness along x.
Multiplier constant for second-order smoothness along x.
Multiplier constant for first-order smoothness along y.
Multiplier constant for second-order smoothness along y.
Multiplier constant for first-order smoothness along z.
Multiplier constant for second-order smoothness along z.
Gradient measure used to update IRLS weights for sparse smoothness.
Scale IRLS weights.
IRLS stabilization constant.
Multiplier constant for smoothness along x relative to base scale length.
Multiplier constant for smoothness along z relative to base scale length.
Multiplier constant for smoothness along z relative to base scale length.
Mapping from the model to the regularization mesh.
The model associated with regularization.
Multiplier constants for weighted sum of objective functions.
Number of model parameters.
Norms for the child regularization classes.
Reference model.
Whether to include the reference model in the smoothness objective functions.
Regularization mesh.
Units for the model parameters.
cell_weights
Methods
__call__(m[, f])Evaluate the objective functions for a given model.
deriv(m[, f])Gradient of the objective function evaluated for the model provided.
deriv2(m[, v, f])Hessian of the objective function evaluated for the model provided.
get_functions_of_type(fun_class)Return objective functions of a given type(s).
map_classremove_weights(key)Removes specified weights from all child regularization objects.
set_weights(**weights)Adds (or updates) the specified weights for all child regularization objects.
test([x, num, random_seed])Run a convergence test on both the first and second derivatives.
update_weights(model)Update IRLS weights for all child regularization objects.
Notes
Sparse regularization can be defined by a weighted sum of
SparseSmallnessandSparseSmoothnessregularization functions. This corresponds to a model objective function \(\phi_m (m)\) of the form:\[\phi_m (m) = \alpha_s \int_\Omega \, w(r) \Big | \, m(r) - m^{(ref)}(r) \, \Big |^{p_s(r)} \, dv + \sum_{j=x,y,z} \alpha_j \int_\Omega \, w(r) \Bigg | \, \frac{\partial m}{\partial \xi_j} \, \Bigg |^{p_j(r)} \, dv\]where \(m(r)\) is the model, \(m^{(ref)}(r)\) is the reference model, and \(w(r)\) is a user-defined weighting function applied to all terms. \(\xi_j\) for \(j=x,y,z\) are unit directions along \(j\). Parameters \(\alpha_s\) and \(\alpha_j\) for \(j=x,y,z\) are multiplier constants that weight the respective contributions of the smallness and smoothness terms in the regularization. \(p_s(r) \in [0,2]\) is a parameter which imposes sparse smallness throughout the recovered model; where more compact structures are recovered in regions where \(p_s(r)\) is small. And \(p_j(r) \in [0,2]\) for \(j=x,y,z\) are parameters which impose sparse smoothness throughout the recovered model along the specified direction; where sharper boundaries are recovered in regions where these parameters are small.
For implementation within SimPEG, regularization functions and their variables must be discretized onto a mesh. For a regularization function whose kernel is given by \(f(r)\), we approximate as follows:
\[\int_\Omega w(r) \big [ f(r) \big ]^{p(r)} \, dv \approx \sum_i \tilde{w}_i \, | f_i |^{p_i}\]where \(f_i \in \mathbf{f_m}\) define the discrete regularization kernel function on the mesh. For example, the regularization kernel function for smallness regularization is:
\[\mathbf{f_m}(\mathbf{m}) = \mathbf{m - m}^{(ref)}\]\(\tilde{w}_i \in \mathbf{\tilde{w}}\) are amalgamated weighting constants that 1) account for cell dimensions in the discretization and 2) apply user-defined weighting. \(p_i \in \mathbf{p}\) define the sparseness throughout the domain (set using norm).
It is impractical to work with sparse norms directly, as their derivatives with respect to the model are non-linear and discontinuous. Instead, the iteratively re-weighted least-squares (IRLS) approach is used to approximate sparse norms by iteratively solving a set of convex least-squares problems. For IRLS iteration \(k\), we define:
\[\sum_i \tilde{w}_i \, \Big | f_i^{(k)} \Big |^{p_i} \approx \sum_i \tilde{w}_i \, r_i^{(k)} \Big | f_i^{(k)} \Big |^2\]where the IRLS weight \(r_i\) for iteration \(k\) is given by:
\[r_i^{(k)} = \bigg [ \Big ( f_i^{(k-1)} \Big )^2 + \epsilon^2 \; \bigg ]^{p_i/2 - 1}\]and \(\epsilon\) is a small constant added for stability (set using irls_threshold). For the set of model parameters \(\mathbf{m}\) defined at cell centers, the model objective function for IRLS iteration \(k\) can be expressed as a weighted sum of objective functions of the form:
\[\phi_m (\mathbf{m}) = \alpha_s \Big \| \mathbf{W_s}^{\!\! (k)} \big [ \mathbf{m} - \mathbf{m}^{(ref)} \big ] \Big \|^2 + \sum_{j=x,y,z} \alpha_j \Big \| \mathbf{W_j}^{\! (k)} \mathbf{G_j \, m} \Big \|^2\]where
\(\mathbf{m}\) are the set of discrete model parameters (i.e. the model),
\(\mathbf{m}^{(ref)}\) is the reference model,
\(\mathbf{G_x, \, G_y, \; G_z}\) are partial cell gradients operators along x, y and z, and
\(\mathbf{W_s, \, W_x, \, W_y, \; W_z}\) are the weighting matrices for iteration \(k\).
The weighting matrices apply the IRLS weights, user-defined weighting, and account for cell dimensions when the regularization functions are discretized.
IRLS weights, user-defined weighting and the weighting matrix:
Let \(\mathbf{w_1, \; w_2, \; w_3, \; ...}\) each represent an optional set of custom cell weights that are applied to all objective functions in the model objective function. For IRLS iteration \(k\), the general form for the weights applied to the sparse smallness term is given by:
\[\mathbf{w_s}^{\!\! (k)} = \mathbf{r_s}^{\!\! (k)} \odot \mathbf{v} \odot \prod_j \mathbf{w_j}\]And for sparse smoothness along x (likewise for y and z) is given by:
\[\mathbf{w_x}^{\!\! (k)} = \mathbf{r_x}^{\!\! (k)} \odot \big ( \mathbf{P_x \, v} \big ) \odot \prod_j \mathbf{P_x \, w_j}\]The IRLS weights at iteration \(k\) are defined as \(\mathbf{r_\ast}^{\!\! (k)}\) for \(\ast = s,x,y,z\). \(\mathbf{v}\) are the cell volumes. Operators \(\mathbf{P_\ast}\) for \(\ast = x,y,z\) project to the appropriate faces.
Once the net weights for all objective functions are computed, their weighting matrices can be constructed via:
\[\mathbf{W}_\ast^{(k)} = \textrm{diag} \Big ( \, \sqrt{\mathbf{w_\ast}^{\!\! (k)} \, } \Big )\]Each set of custom cell weights is stored within a
dictas an (n_cells, )numpy.ndarray. The weights can be set all at once during instantiation with the weights keyword argument as follows:>>> reg = Sparse(mesh, weights={'weights_1': array_1, 'weights_2': array_2})
or set after instantiation using the set_weights method:
>>> reg.set_weights(weights_1=array_1, weights_2=array_2})
Reference model in smoothness:
Gradients/interfaces within a discrete reference model can be preserved by including the reference model the smoothness regularization. In this case, the objective function becomes:
\[\phi_m (\mathbf{m}) = \alpha_s \Big \| \mathbf{W_s}^{\! (k)} \big [ \mathbf{m} - \mathbf{m}^{(ref)} \big ] \Big \|^2 + \sum_{j=x,y,z} \alpha_j \Big \| \mathbf{W_j}^{\! (k)} \mathbf{G_j} \big [ \mathbf{m} - \mathbf{m}^{(ref)} \big ] \Big \|^2\]This functionality is used by setting the reference_model_in_smooth parameter to
True.Alphas and length scales:
The \(\alpha\) parameters scale the relative contributions of the smallness and smoothness terms in the model objective function. Each \(\alpha\) parameter can be set directly as an appropriate property of the
WeightedLeastSquaresclass; e.g. \(\alpha_x\) is set using the alpha_x property. Note that unless the parameters are set manually, second-order smoothness is not included in the model objective function. That is, the alpha_xx, alpha_yy and alpha_zz parameters are set to 0 by default.The relative contributions of smallness and smoothness terms on the recovered model can also be set by leaving alpha_s as its default value of 1, and setting the smoothness scaling constants based on length scales. The model objective function has been formulated such that smallness and smoothness terms contribute equally when the length scales are equal; i.e. when properties length_scale_x = length_scale_y = length_scale_z. When the length_scale_x property is set, the alpha_x and alpha_xx properties are set internally as:
>>> reg.alpha_x = (reg.length_scale_x * reg.regularization_mesh.base_length) ** 2.0
and
>>> reg.alpha_xx = (ref.length_scale_x * reg.regularization_mesh.base_length) ** 4.0
Likewise for y and z.
Galleries and Tutorials using simpeg.regularization.Sparse#
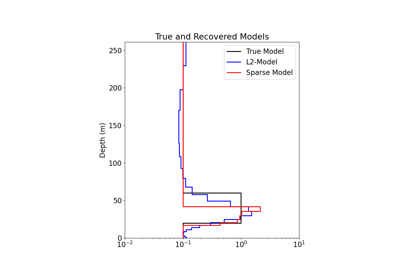
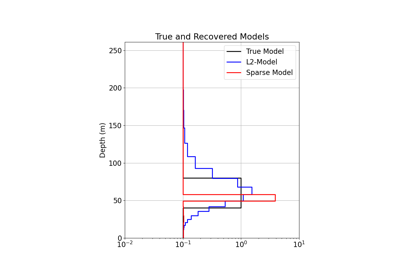
Sparse Inversion with Iteratively Re-Weighted Least-Squares
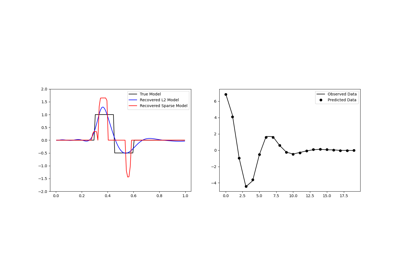
1D Inversion of Time-Domain Data for a Single Sounding
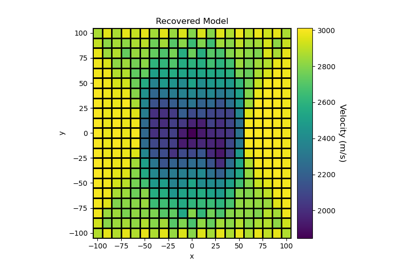
Sparse Norm Inversion of 2D Seismic Tomography Data