simpeg.maps.Projection#

class simpeg.maps.Projection(nP, index, **kwargs)[source]#

Bases: IdentityMap

Projection mapping.

Projection mapping can be used to project and/or rearange model parameters. For a set of model parameter \(\mathbf{m}\), the mapping \(\mathbf{u}(\mathbf{m})\) can be defined by a linear projection matrix \(\mathbf{P}\) acting on the model, i.e.:

\[\mathbf{u}(\mathbf{m}) = \mathbf{Pm}\]

The number of model parameters the mapping acts on is defined by nP. Projection and/or rearrangement of the parameters is defined by index. Thus the dimensions of the mapping is (nInd, nP).

Parameters:

nPint: Number of model parameters the mapping acts on
indexnumpy.ndarray of int: Indexes defining the projection from the model space

Attributes

`is_linear`	Determine whether or not this mapping is a linear operation.
`mesh`	The mesh used for the mapping
`nP`	Number of parameters the mapping acts on.
`shape`	Dimensions of the mapping.

Methods

`deriv`(m[, v])	Derivative of the mapping with respect to the input parameters.
`dot`(map1)	Multiply two mappings to create a `simpeg.maps.ComboMap`.
`inverse`(D)	The transform inverse is not implemented.
`test`([m, num, random_seed])	Derivative test for the mapping.

Examples

Here we define a mapping that rearranges and projects 2 model parameters to a vector space spanning 4 parameters.

>>> from simpeg.maps import Projection
>>> import numpy as np

>>> nP = 2
>>> index = np.array([1, 0, 1, 0], dtype=int)
>>> mapping = Projection(nP, index)

>>> m = np.array([6, 8])
>>> mapping * m
array([8, 6, 8, 6])

Galleries and Tutorials using `simpeg.maps.Projection`#

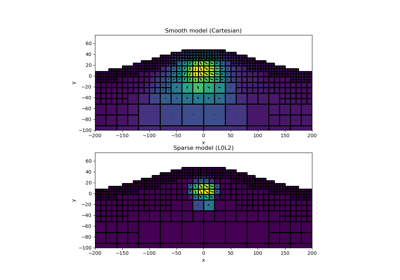
Magnetic inversion on a TreeMesh with remanence

Petrophysically guided inversion: Joint linear example with nonlinear relationships

Heagy et al., 2017 Casing Example

Tensor Meshes

Cylindrical Meshes

Tree Meshes

Cross-gradient Joint Inversion of Gravity and Magnetic Anomaly Data

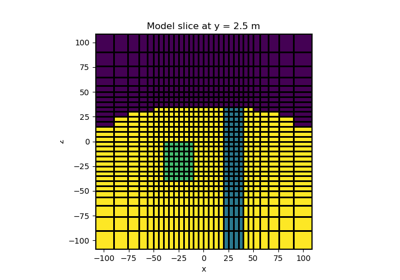
Joint PGI of Gravity + Magnetic on an Octree mesh using full petrophysical information

Joint PGI of Gravity + Magnetic on an Octree mesh without petrophysical information

simpeg.maps.Projection#

Galleries and Tutorials using simpeg.maps.Projection#

This Page

Galleries and Tutorials using `simpeg.maps.Projection`#