SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation#
- class SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation(mesh, survey=None, forward_only=False, **kwargs)[source]#
Bases:
SimPEG.electromagnetics.base.BaseEMSimulationWe start by looking at Maxwell’s equations in the electric field \(\mathbf{e}\) and the magnetic flux density \(\mathbf{b}\)
\[\begin{split}\mathbf{C} \mathbf{e} + i \omega \mathbf{b} = \mathbf{s_m} \\ {\mathbf{C}^{\top} \mathbf{M_{\mu^{-1}}^f} \mathbf{b} - \mathbf{M_{\sigma}^e} \mathbf{e} = \mathbf{s_e}}\end{split}\]if using the E-B formulation (
Simulation3DElectricFieldorSimulation3DMagneticFluxDensity). Note that in this case, \(\mathbf{s_e}\) is an integrated quantity.If we write Maxwell’s equations in terms of \(\mathbf{h}\) and current density \(\mathbf{j}\)
\[\begin{split}\mathbf{C}^{\top} \mathbf{M_{\rho}^f} \mathbf{j} + i \omega \mathbf{M_{\mu}^e} \mathbf{h} = \mathbf{s_m} \\ \mathbf{C} \mathbf{h} - \mathbf{j} = \mathbf{s_e}\end{split}\]if using the H-J formulation (
Simulation3DCurrentDensityorSimulation3DMagneticField). Note that here, \(\mathbf{s_m}\) is an integrated quantity.The problem performs the elimination so that we are solving the system for \(\mathbf{e},\mathbf{b},\mathbf{j} \) or \(\mathbf{h}\)
Attributes
If True, A-inverse not stored at each frequency in forward simulation.
The simulations survey.
Methods
Jtvec(m, v[, f])Sensitivity transpose times a vector
Jvec(m, v[, f])Sensitivity times a vector.
fields([m])Solve the forward problem for the fields.
fieldsPairalias of
SimPEG.electromagnetics.frequency_domain.fields.FieldsFDEMgetSourceTerm(freq)Evaluates the sources for a given frequency and puts them in matrix form
Galleries and Tutorials using SimPEG.electromagnetics.frequency_domain.simulation.BaseFDEMSimulation#
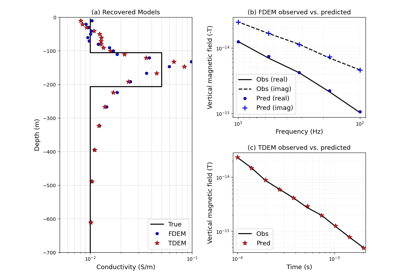
Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion