SimPEG.regularization.Sparse#
- class SimPEG.regularization.Sparse(mesh, active_cells=None, norms=None, gradient_type='total', irls_scaled=True, irls_threshold=1e-08, **kwargs)[source]#
Bases:
SimPEG.regularization.base.WeightedLeastSquaresThe regularization is:
\[R(m) = \frac{1}{2}\mathbf{(m-m_\text{ref})^\top W^\top R^\top R W(m-m_\text{ref})}\]where the IRLS weight
\[R = \eta \text{diag} \left[\mathbf{r}_s \right]^{1/2} \ r_{s_i} = {\Big( {({m_i}^{(k-1)})}^{2} + \epsilon^2 \Big)}^{p_s/2 - 1}\]where k denotes the iteration number. So the derivative is straight forward:
\[R(m) = \mathbf{W^\top R^\top R W (m-m_\text{ref})}\]The IRLS weights are re-computed after each beta solves using
Update_IRLSwithin the inversion directives.Attributes
0.gradientType has been deprecated.
Choice of gradient measure used in the irls weights
Scale irls weights.
Constant added to the denominator of the IRLS weights for stability.
Value of the norm
Methods
update_weights(model)Trigger irls update on all children
Galleries and Tutorials using SimPEG.regularization.Sparse#
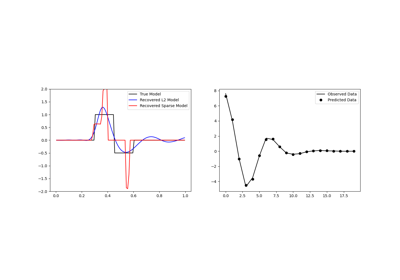
Sparse Inversion with Iteratively Re-Weighted Least-Squares
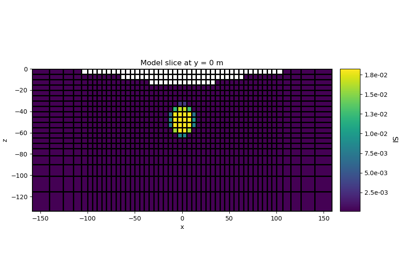
Sparse Norm Inversion for Total Magnetic Intensity Data on a Tensor Mesh
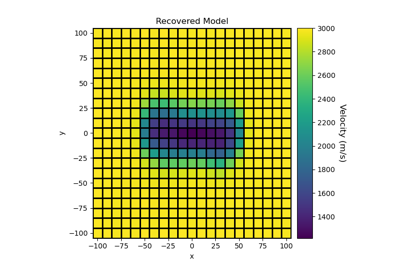
Sparse Norm Inversion of 2D Seismic Tomography Data
1D Inversion of Time-Domain Data for a Single Sounding