simpeg.electromagnetics.frequency_domain.Simulation3DMagneticFluxDensity#
- class simpeg.electromagnetics.frequency_domain.Simulation3DMagneticFluxDensity(mesh, survey=None, forward_only=False, permittivity=None, storeJ=False, **kwargs)[source]#
Bases:
BaseFDEMSimulation3D FDEM simulation in terms of the magnetic flux field.
This simulation solves for the magnetic flux density at each frequency. In this formulation, the electric fields are defined on mesh edges and the magnetic flux density is defined on mesh faces; i.e. it is an EB formulation. See the Notes section for a comprehensive description of the formulation.
- Parameters:
- mesh
discretize.base.BaseMesh The mesh.
- survey
frequency_domain.survey.Survey The frequency-domain EM survey.
- forward_onlybool,
optional If
True, the factorization for the inverse of the system matrix at each frequency is discarded after the fields are computed at that frequency. IfFalse, the factorizations of the system matrices for all frequencies are stored.- permittivity(n_cells,)
numpy.ndarray,optional Dielectric permittivity (F/m) defined on the entire mesh. If
None, electric displacement is ignored. Please note that permittivity is not an invertible property, and that future development will result in the deprecation of this propery.- storeJbool,
optional Whether to compute and store the sensitivity matrix.
- mesh
Attributes
Cell center inner product matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Cell center property inner product matrix.
Cell center property inner product inverse matrix.
Edge inner product matrix.
Edge inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Edge property inner product matrix.
Edge property inner product inverse matrix.
Face inner product matrix.
Face inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Face property inner product matrix.
Face property inner product inverse matrix.
Node inner product matrix.
Node inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
Node property inner product matrix.
Node property inner product inverse matrix.
A list of solver objects to clean when the model is updated
SimPEG
Counterobject to store iterations and run-times.HasModel.deleteTheseOnModelUpdate has been deprecated.
Whether to store the factorizations of the inverses of the system matrices.
Mesh for the simulation.
The inversion model.
Magnetic permeability (h/m) physical property model.
Derivative of Magnetic Permeability (H/m) wrt the model.
Mapping of the inversion model to Magnetic Permeability (H/m).
Inverse magnetic permeability (m/h) physical property model.
Derivative of Inverse Magnetic Permeability (m/H) wrt the model.
Mapping of the inversion model to Inverse Magnetic Permeability (m/H).
True if a model is necessary
Dielectric permittivity (F/m)
Electrical resistivity (ohm m) physical property model.
Derivative of Electrical resistivity (Ohm m) wrt the model.
Mapping of the inversion model to Electrical resistivity (Ohm m).
Path to directory where sensitivity file is stored.
Electrical conductivity (s/m) physical property model.
Derivative of Electrical conductivity (S/m) wrt the model.
Mapping of the inversion model to Electrical conductivity (S/m).
Numerical solver used in the forward simulation.
Solver-specific parameters.
Whether to store inner product matrices
Whether to compute and store the sensitivity matrix.
The FDEM survey object.
Verbose progress printout.
MccI
Vol
Methods
Jtvec(m, v[, f])Compute the adjoint sensitivity matrix times a vector.
Jtvec_approx(m, v[, f])Approximation of the Jacobian transpose times a vector for the model provided.
Jvec(m, v[, f])Compute the sensitivity matrix times a vector.
Jvec_approx(m, v[, f])Approximation of the Jacobian times a vector for the model provided.
MccMuDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccMuIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccMuiDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccMuiIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccRhoDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccRhoIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MccSigmaDeriv(u[, v, adjoint])Derivative of MccProperty with respect to the model.
MccSigmaIDeriv(u[, v, adjoint])Derivative of MccPropertyI with respect to the model.
MeMuDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeMuIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeMuiDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeMuiIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeRhoDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeRhoIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MeSigmaDeriv(u[, v, adjoint])Derivative of MeProperty with respect to the model.
MeSigmaIDeriv(u[, v, adjoint])Derivative of MePropertyI with respect to the model.
MfMuDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfMuIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfMuiDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfMuiIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfRhoDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfRhoIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MfSigmaDeriv(u[, v, adjoint])Derivative of MfProperty with respect to the model.
MfSigmaIDeriv(u[, v, adjoint])I Derivative of MfPropertyI with respect to the model.
MnMuDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnMuIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnMuiDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnMuiIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnRhoDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnRhoIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
MnSigmaDeriv(u[, v, adjoint])Derivative of MnProperty with respect to the model.
MnSigmaIDeriv(u[, v, adjoint])Derivative of MnPropertyI with respect to the model.
dpred([m, f])Predicted data for the model provided.
fields([m])Compute and return the fields for the model provided.
fieldsPairalias of
Fields3DMagneticFluxDensitygetA(freq)System matrix for the frequency provided.
getADeriv(freq, u, v[, adjoint])Derivative operation for the system matrix times a vector.
getADeriv_mui(freq, u, v[, adjoint])Inverse permeability derivative operation for the system matrix times a vector.
getADeriv_sigma(freq, u, v[, adjoint])Conductivity derivative operation for the system matrix times a vector.
getJ(m[, f])Generate the full sensitivity matrix.
getJtJdiag(m[, W, f])Return the diagonal of \(\mathbf{J^T J}\).
getRHS(freq)Right-hand sides for the given frequency.
getRHSDeriv(freq, src, v[, adjoint])Derivative of the right-hand side times a vector for a given source and frequency.
getSourceTerm(freq)Returns the discrete source terms for the frequency provided.
make_synthetic_data(m[, relative_error, ...])Make synthetic data for the model and Gaussian noise provided.
residual(m, dobs[, f])The data residual.
Notes
Here, we start with the Maxwell’s equations in the frequency-domain where a \(+i\omega t\) Fourier convention is used:
\[\begin{split}\begin{align} &\nabla \times \vec{E} + i\omega \vec{B} = - i \omega \vec{S}_m \\ &\nabla \times \vec{H} - \vec{J} = \vec{S}_e \end{align}\end{split}\]where \(\vec{S}_e\) is an electric source term that defines a source current density, and \(\vec{S}_m\) magnetic source term that defines a source magnetic flux density. We define the constitutive relations for the electrical conductivity \(\sigma\) and magnetic permeability \(\mu\) as:
\[\begin{split}\vec{J} &= \sigma \vec{E} \\ \vec{H} &= \mu^{-1} \vec{B}\end{split}\]We then take the inner products of all previous expressions with a vector test function \(\vec{u}\). Through vector calculus identities and the divergence theorem, we obtain:
\[\begin{split}& \int_\Omega \vec{u} \cdot (\nabla \times \vec{E}) \, dv + i \omega \int_\Omega \vec{u} \cdot \vec{B} \, dv = - i \omega \int_\Omega \vec{u} \cdot \vec{S}_m \, dv \\ & \int_\Omega (\nabla \times \vec{u}) \cdot \vec{H} \, dv - \oint_{\partial \Omega} \vec{u} \cdot (\vec{H} \times \hat{n}) \, da - \int_\Omega \vec{u} \cdot \vec{J} \, dv = \int_\Omega \vec{u} \cdot \vec{S}_j \, dv \\ & \int_\Omega \vec{u} \cdot \vec{J} \, dv = \int_\Omega \vec{u} \cdot \sigma \vec{E} \, dv \\ & \int_\Omega \vec{u} \cdot \vec{H} \, dv = \int_\Omega \vec{u} \cdot \mu^{-1} \vec{B} \, dv\end{split}\]Assuming natural boundary conditions, the surface integral is zero.
The above expressions are discretized in space according to the finite volume method. The discrete electric fields \(\mathbf{e}\) are defined on mesh edges, and the discrete magnetic flux densities \(\mathbf{b}\) are defined on mesh faces. This implies \(\mathbf{j}\) must be defined on mesh edges and \(\mathbf{h}\) must be defined on mesh faces. Where \(\mathbf{u_e}\) and \(\mathbf{u_f}\) represent test functions discretized to edges and faces, respectively, we obtain the following set of discrete inner-products:
\[\begin{split}&\mathbf{u_f^T M_f C e} + i \omega \mathbf{u_f^T M_f b} = - i \omega \mathbf{u_f^T M_f s_m} \\ &\mathbf{u_e^T C^T M_f h} - \mathbf{u_e^T M_e j} = \mathbf{u_e^T s_e} \\ &\mathbf{u_e^T M_e j} = \mathbf{u_e^T M_{e\sigma} e} \\ &\mathbf{u_f^T M_f h} = \mathbf{u_f^T M_{f \mu} b}\end{split}\]where
\(\mathbf{C}\) is the discrete curl operator
\(\mathbf{s_m}\) and \(\mathbf{s_e}\) are the integrated magnetic and electric source terms, respectively
\(\mathbf{M_e}\) is the edge inner-product matrix
\(\mathbf{M_f}\) is the face inner-product matrix
\(\mathbf{M_{e\sigma}}\) is the inner-product matrix for conductivities projected to edges
\(\mathbf{M_{f\frac{1}{\mu}}}\) is the inner-product matrix for inverse permeabilities projected to faces
By cancelling like-terms and combining the discrete expressions to solve for the magnetic flux density, we obtain:
\[\mathbf{A \, b} = \mathbf{q}\]where
\(\mathbf{A} = \mathbf{C M_{e\sigma}^{-1} C^T M_{f\frac{1}{\mu}}} + i\omega \mathbf{I}\)
\(\mathbf{q} = \mathbf{C M_{e\sigma}^{-1} s_e} - i \omega \mathbf{s_m}\)
Galleries and Tutorials using simpeg.electromagnetics.frequency_domain.Simulation3DMagneticFluxDensity#
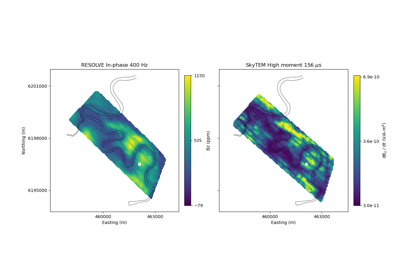
Heagy et al., 2017 1D RESOLVE and SkyTEM Bookpurnong Inversions
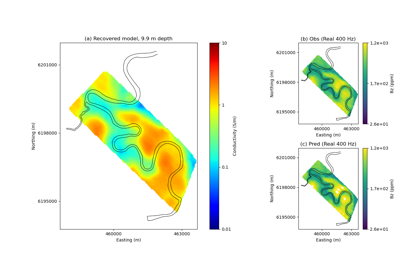
Heagy et al., 2017 1D RESOLVE Bookpurnong Inversion